题目内容
15.已知$sin2θ-4sin({θ+\frac{π}{3}})sin({θ-\frac{π}{6}})=\frac{{\sqrt{3}}}{3}$,则cos2θ等于( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $-\frac{{\sqrt{3}}}{6}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
分析 直接由三角函数的诱导公式化简计算得答案.
解答 解:$sin2θ-4sin(θ+\frac{π}{3})sin(θ-\frac{π}{6})$=$sin2θ-4sin({θ-\frac{π}{6}})cos({θ-\frac{π}{6}})=sin2θ-2sin({2θ-\frac{π}{3}})=\sqrt{3}cos2θ=\frac{{\sqrt{3}}}{3}$,
即$cos2θ=\frac{1}{3}$.
故选:B.
点评 本题考查了三角函数的化简求值,考查了三角函数的诱导公式的应用,是基础题.

练习册系列答案
相关题目
5.不等式ax2+bx+c<0的解集为空集,则( )
| A. | a<0,△>0 | B. | a<0,△≥0 | C. | a>0,△≤0 | D. | a>0,△≥0 |
3.已知sin(3π+α)=2sin$({\frac{3π}{2}+α})$,求下列各式的值:
(1)$\frac{2sinα-3cosα}{4sinα-9cosα}$;
(2)sin2α+sin 2α.
(1)$\frac{2sinα-3cosα}{4sinα-9cosα}$;
(2)sin2α+sin 2α.
7.下列命题正确的是( )
| A. | 若a2>b2,则a>b | B. | 若ac>bc,则a>b | C. | 若$\frac{1}{a}>\frac{1}{b},则a<b$ | D. | 若$\sqrt{a}<\sqrt{b},则a<b$ |
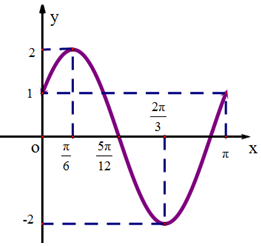 已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<\frac{π}{2})$的部分图象如图所示.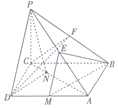 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是矩形,BC=PC,E,F分别是PA,PB的中点. 如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.
如图,已知平面ABC⊥平面BCDE,△DEF与△ABC分别是棱长为1与2的正三角形,AC∥DF,四边形BCDE为直角梯形,DE∥BC,BC⊥CD,CD=1,点G为△ABC的重心,N为AB中点,$\overrightarrow{AM}=λ\overrightarrow{AF}(λ∈R,λ>0)$.