Question

|

OA

|=1，|

OB

|=

3

，

OA

与

OB

的夹角为150°，点C是△ABO的外接圆优弧

AB

上的一个动点，则

OA

•

OC

的最大值

 

．

Answer 1

考点：平面向量数量积的运算

专题：计算题,平面向量及应用,直线与圆

分析：建立直角坐标系，写出A（1，0），B（-

3

2

，

3

2

），O（0，0），求出圆的方程为x²+y²-x-3

3

y=0，则

OA

•

OC

=x，即圆上的点的横坐标，即可得到最大值．

解答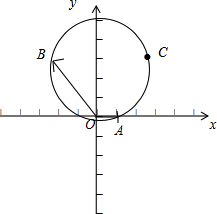： 解：如图，建立直角坐标系，
则A（1，0），B（-

3

2

，

3

2

），O（0，0），
设C（x，y），圆的方程为：x²+y²+Dx+Ey+F=0，
将A（1，0），B（-

3

2

，

3

2

），C（x，y）代入圆的方程，
解得D=-1，E=-3

3

，F=0；
∴x²+y²-x-3

3

y=0，
表示圆心为（

1

2

，

3 3

2

），半径为

7

的圆，
则

OA

•

OC

=x，
∴x的最大值为

1

2

+

7

，
故答案为：

1

2

+

7

．

点评：本题考查圆的方程及向量的数量积，考查利用代数解决几何问题的方法，属于中档题．