题目内容
1.如图,OABC是四面体,G是△ABC的重心,G2是OG上一点,且OG=3OG1,则( )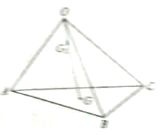
| A. | $\overrightarrow{O{G_1}}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ | B. | $\overrightarrow{O{G_1}}=\frac{1}{9}\overrightarrow{OA}+\frac{1}{9}\overrightarrow{OB}+\frac{1}{9}\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G_1}}=\frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$ | D. | $\overrightarrow{O{G_1}}=\frac{3}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}+\frac{3}{4}\overrightarrow{OC}$ |
分析 利用空间向量加法法则求解.
解答 解:∵OABC是四面体,G是△ABC的重心,G2是OG上一点,且OG=3OG1,
∴$\overrightarrow{O{G}_{1}}$=$\frac{1}{3}\overrightarrow{OG}$=$\frac{1}{3}$($\overrightarrow{OA}+\overrightarrow{AG}$)=$\frac{1}{3}\overrightarrow{OA}$+$\frac{1}{3}$[$\frac{1}{3}(\overrightarrow{AB}+\overrightarrow{AC})$]
=$\frac{1}{3}\overrightarrow{OA}$+$\frac{1}{9}$($\overrightarrow{OB}-\overrightarrow{OA}$)+$\frac{1}{9}$($\overrightarrow{OC}-\overrightarrow{OA}$)=$\frac{1}{9}\overrightarrow{OA}+\frac{1}{9}\overrightarrow{OB}+\frac{1}{9}\overrightarrow{OC}$.
故选:B.
点评 本题考查向量的求法,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.执行如图所示的程序框图,则输出y的值为( )
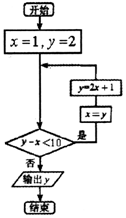

| A. | 5 | B. | 11 | C. | 23 | D. | 47 |
13.如果直线x=ky-1与圆C:x2+y2+kx+my+2p=0相交,且两个交点关于直线y=x对称,那么实数p的取值范围是( )
| A. | $({-∞,-\frac{3}{2}})$ | B. | $({-∞,-\frac{3}{4}})$ | C. | $({-\frac{3}{4},+∞})$ | D. | $({-\frac{3}{2},+∞})$ |
10.数列{an}的通项an是关于x的不等式x2-x<nx(n∈N*)的解集中的整数个数,则数列{an}的前n项和Sn=( )
| A. | n2 | B. | n(n+1) | C. | $\frac{n(n+1)}{2}$ | D. | (n+1)(n+2) |
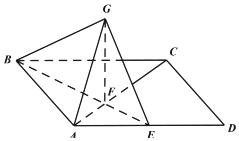 如图,四边形 ABCD是平行四边形,AB=1,AD=2,AC=$\sqrt{3}$,E 是 AD的中点,BE与AC 交于点F,GF⊥平面ABCD.
如图,四边形 ABCD是平行四边形,AB=1,AD=2,AC=$\sqrt{3}$,E 是 AD的中点,BE与AC 交于点F,GF⊥平面ABCD.