题目内容
10.数列{an}的通项an是关于x的不等式x2-x<nx(n∈N*)的解集中的整数个数,则数列{an}的前n项和Sn=( )| A. | n2 | B. | n(n+1) | C. | $\frac{n(n+1)}{2}$ | D. | (n+1)(n+2) |
分析 通过解不等式求出数列{an}的通项an判断数列{an}是什么数列,即可数列{an}的前n项和Sn
解答 解:不等式x2-x<nx(n∈N*)的解集为{x|0<x<n+1}
∵通项an是解集中的整数个数
∴an=n(n∈N*)
∵an+1-an=n+1-n=1(常数),
∴数列{an}是首先为1,公差为1的等差数列.
∴前n项和Sn=$\frac{n(n+1)}{2}$.
故选C
点评 本题主要考查数列通项公式和前n项和的求解,求解不等式的解集中的整数个数得到an是解决本题的关键.

练习册系列答案
相关题目
1.如图,OABC是四面体,G是△ABC的重心,G2是OG上一点,且OG=3OG1,则( )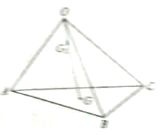

| A. | $\overrightarrow{O{G_1}}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ | B. | $\overrightarrow{O{G_1}}=\frac{1}{9}\overrightarrow{OA}+\frac{1}{9}\overrightarrow{OB}+\frac{1}{9}\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G_1}}=\frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$ | D. | $\overrightarrow{O{G_1}}=\frac{3}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}+\frac{3}{4}\overrightarrow{OC}$ |
18.在长方体ABCD-A1B1C1D1中,A1A=AB=2BC=2,则异面直线AC与BD1所成角的余弦值是( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{5}$ | D. | $\frac{\sqrt{5}}{3}$ |
5.已知函数f(x)=$\frac{1}{3}$x3-mx2+x+2有两个极值点,则m的取值范围是( )
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1)∪(1,+∞) |
8.某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩单(单位:分),并列成如表所示的频数分布表:
(1)试估计该年级成绩≥80分的学生人数;
(2)已知样本在成绩在[40,50)中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
| 组别 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 6 | 18 | 28 | 26 | 17 | 5 |
(2)已知样本在成绩在[40,50)中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
9.下列函数中,在区间(0,+∞)上为增函数的是( )
| A. | y=lg(x+1) | B. | y=tanx | C. | y=2-x | D. | y=x-2 |