题目内容

20．已知$\overrightarrow{AB}$=$\overrightarrow{a}$+5$\overrightarrow{b}$，$\overrightarrow{BC}$=-2$\overrightarrow{a}$+8$\overrightarrow{b}$，$\overrightarrow{CD}$=λ（$\overrightarrow{a}$-$\overrightarrow{b}$），且A、B、D三点共线，则λ的值为（　　）
A．3B．-3C．2D．-2

分析 由题意，$\overrightarrow{BD}$=（λ-2）$\overrightarrow{a}$+（8-λ）$\overrightarrow{b}$，利用A、B、D三点共线，可得方程，即可得出结论．

解答 解：由题意，$\overrightarrow{BD}$=（λ-2）$\overrightarrow{a}$+（8-λ）$\overrightarrow{b}$，
∵A、B、D三点共线，
∴1×（8-λ）=5×（λ-2），
∴λ=3，
故选A．

点评 本题考查三点共线，考查向量知识的运用，比较基础．

练习册系列答案
相关题目
1．如图，OABC是四面体，G是△ABC的重心，G2是OG上一点，且OG=3OG1，则（　　）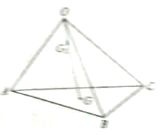
A．$\overrightarrow{O{G_1}}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$B．$\overrightarrow{O{G_1}}=\frac{1}{9}\overrightarrow{OA}+\frac{1}{9}\overrightarrow{OB}+\frac{1}{9}\overrightarrow{OC}$
C．$\overrightarrow{O{G_1}}=\frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$D．$\overrightarrow{O{G_1}}=\frac{3}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}+\frac{3}{4}\overrightarrow{OC}$
11．已知各项均为正数的等比数列{an}的前n项和为Sn，若a5=2a3+a4，且S5=62．
（1）求数列{an}的通项公式；
（2）设bn=$\frac{{a}_{n+1}}{{S}_{n}{S}_{n+1}}$，数列{bn}的前n项和为Tn，求证：$\frac{1}{3}$≤Tn＜$\frac{1}{2}$．
8．某校高三共有2000名学生参加广安市联考，现随机抽取100名学生的成绩单（单位：分），并列成如表所示的频数分布表：
组别[40，50）[50，60）[60，70）[70，80）[80，90）[90，100]
频数6182826175
（1）试估计该年级成绩≥80分的学生人数；
（2）已知样本在成绩在[40，50）中的6名学生中，有4名男生，2名女生，现从中选2人进行调研，求恰好选中一名男生一名女生的概率．
15．已知抛物线C：y2=-4x的焦点为F，A（-2，1），P为抛物线C上的动点，则|PF|+|PA|的最小值为3．
5．已知f（a）=$\frac{si{n}^{2}（π-α）•cos（2π-α）•tan（-π+α）}{sin（-π+α）•tan（-α+3π）}$．
（1）化简f（α）；
（2）若f（α）=$\frac{1}{8}$，且$\frac{π}{4}$＜α＜$\frac{π}{2}$，求cosα-sinα的值；
（3）若α=-$\frac{31π}{3}$，求f（α）的值．
12．已知直线l过点（0，5），且在两坐标轴上的截距之和为2．
（1）求直线l的方程；
（2）若直线l1过点（$\frac{8}{3}$，-1）且与直线l垂直，直线l2与直线l1关于x轴对称，求直线l2的方程．
9．下列函数中，在区间（0，+∞）上为增函数的是（　　）
A．y=lg（x+1）B．y=tanxC．y=2-xD．y=x-2
10．下列有关命题的叙述，其中错误的个数为（　　）
①若p∨q为真命题，则p∧q也为真命题
②“x＞5”是“x2-4x-5＞0”的充分不必要条件
③命题：?x∈R，2x＞x2的否定为：?x0∉R，2${\;}^{{x}_{0}}$≤x02；
④?x∈R，使得ex=1+x是真命题．
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网