题目内容
9.已知a,b∈R,若点M(1,2)在矩阵A=$[\begin{array}{l}{a}&{1}\\{b}&{4}\end{array}]$对应的变换作用下得到点N(2,-7),求矩阵A的特征值.分析 先求出矩阵A,再利用矩阵A的特征多项式f(λ)=$|\begin{array}{l}{λ-4}&{-1}\\{-1}&{λ-4}\end{array}|$=(λ-3)(λ-5)=0,求矩阵A的特征值.
解答 解:由题意得$[\begin{array}{l}{a}&{1}\\{b}&{4}\end{array}]$$[\begin{array}{l}{1}\\{-2}\end{array}]$=$[\begin{array}{l}{2}\\{-7}\end{array}]$,∴$\left\{\begin{array}{l}{a-2=2}\\{b-8=-7}\end{array}\right.$,∴a=4,b=1,
∴A=$[\begin{array}{l}{4}&{1}\\{1}&{4}\end{array}]$,
∴矩阵A的特征多项式f(λ)=$|\begin{array}{l}{λ-4}&{-1}\\{-1}&{λ-4}\end{array}|$=(λ-3)(λ-5),
由f(λ)=0,可得λ=3或5.
点评 本题考查矩阵变换,考查特征多项式的运用,属于中档题.

练习册系列答案
相关题目
17.一片森林原有面积为a,现计划每年采伐一些树木,且每年采伐的森林面积占上一年底森林面积的百分比为q,即第x(x∈N)年底的剩余森林面积为y=a(1-q)x,x与y的部分对应值如表:
(1)求原有森林面积a和每年采伐森林面积的百分比q;
(2)问经过多少年后,剩余的森林面积开始小于原来的$\frac{1}{10}$.
(注:lg2≈0.301,lg3≈0.477)
| x | 0 | 1 | 2 |
| y | a | $\frac{20}{3}$ | $\frac{40}{9}$ |
(2)问经过多少年后,剩余的森林面积开始小于原来的$\frac{1}{10}$.
(注:lg2≈0.301,lg3≈0.477)
14.已知实数x,y满足$\left\{\begin{array}{l}x+y-4≤0\\ x-y≤0\\ x≥1\end{array}\right.$,则z=2x+3y的最大值为( )
| A. | 5 | B. | 8 | C. | 10 | D. | 11 |
1.如图,OABC是四面体,G是△ABC的重心,G2是OG上一点,且OG=3OG1,则( )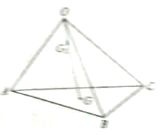

| A. | $\overrightarrow{O{G_1}}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ | B. | $\overrightarrow{O{G_1}}=\frac{1}{9}\overrightarrow{OA}+\frac{1}{9}\overrightarrow{OB}+\frac{1}{9}\overrightarrow{OC}$ | ||
| C. | $\overrightarrow{O{G_1}}=\frac{1}{3}\overrightarrow{OA}+\frac{1}{3}\overrightarrow{OB}+\frac{1}{3}\overrightarrow{OC}$ | D. | $\overrightarrow{O{G_1}}=\frac{3}{4}\overrightarrow{OA}+\frac{3}{4}\overrightarrow{OB}+\frac{3}{4}\overrightarrow{OC}$ |
18.在长方体ABCD-A1B1C1D1中,A1A=AB=2BC=2,则异面直线AC与BD1所成角的余弦值是( )
| A. | $\frac{\sqrt{5}}{5}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{5}$ | D. | $\frac{\sqrt{5}}{3}$ |
8.某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩单(单位:分),并列成如表所示的频数分布表:
(1)试估计该年级成绩≥80分的学生人数;
(2)已知样本在成绩在[40,50)中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
| 组别 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
| 频数 | 6 | 18 | 28 | 26 | 17 | 5 |
(2)已知样本在成绩在[40,50)中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
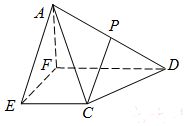 如图,在四棱锥A-CDFE中,底面CDFE是直角梯形,CE∥DF,EF⊥EC,$CE=\frac{1}{2}DF$,AF⊥平面CDFE,P为AD中点.
如图,在四棱锥A-CDFE中,底面CDFE是直角梯形,CE∥DF,EF⊥EC,$CE=\frac{1}{2}DF$,AF⊥平面CDFE,P为AD中点.