题目内容
已知二次函数f(x)的二次项的系数为a,不等式f(x)>-2x的解集为(1,3)
(Ⅰ)若函数y=f(x)+6a有且只有一个零点,求f(x)的解析式;
(Ⅱ)记f(x)的最大值为g(a),求g(a)的最小值.
(Ⅰ)若函数y=f(x)+6a有且只有一个零点,求f(x)的解析式;
(Ⅱ)记f(x)的最大值为g(a),求g(a)的最小值.
考点:二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)由题意可得f(x)+2x=a(x-1)(x-3),a<0.可得f(x)=ax2-(2+4a)x+3a.再根据判别式△=0,求得a的值,可得函数f(x)的解析式.
(Ⅱ)由函数f(x)的解析式 可得g(a)=-a+
-4,利用基本不等式求得g(a)的最小值.
(Ⅱ)由函数f(x)的解析式 可得g(a)=-a+
| 1 |
| -a |
解答:
解:(Ⅰ)因为f(x)>-2x的解集为(1,3),所以f(x)+2x=a(x-1)(x-3),a<0.
于是f(x)=ax2-(2+4a)x+3a.
因为函数y=f(x)+6a有且只有一个零点,∴方程ax2-(2+4a)x+9a=0有两个相等的实数根.
∴△=[-(2+4a)]2-4a•9a=0.即5a2-4a-1=0,解得a=1,或a=-
.
由于a<0,所以a=-
,∴f(x)=-
x2-
x-
.
(Ⅱ)因为f(x)=ax2-(2+4a)x+3a且a<0,
所以g(a)=
=-
=-a+
-4.
∵a<0,所以-a>0,∴g(a)=-a+
-4≥2-4=-2,
当且仅当-a=
,即a=-1时取等号.
所以g(a)的最小值为-2.
于是f(x)=ax2-(2+4a)x+3a.
因为函数y=f(x)+6a有且只有一个零点,∴方程ax2-(2+4a)x+9a=0有两个相等的实数根.
∴△=[-(2+4a)]2-4a•9a=0.即5a2-4a-1=0,解得a=1,或a=-
| 1 |
| 5 |
由于a<0,所以a=-
| 1 |
| 5 |
| 1 |
| 5 |
| 6 |
| 5 |
| 3 |
| 5 |
(Ⅱ)因为f(x)=ax2-(2+4a)x+3a且a<0,
所以g(a)=
| 4a×3a-(2+4a)2 |
| 4a |
| a2+4a+1 |
| a |
| 1 |
| -a |
∵a<0,所以-a>0,∴g(a)=-a+
| 1 |
| -a |
当且仅当-a=
| 1 |
| -a |
所以g(a)的最小值为-2.
点评:本题主要考查二次函数的性质、基本不等式的应用,属于基础题.

练习册系列答案
相关题目
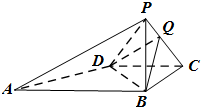 已知四面体P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD=
已知四面体P-ABCD中,PB⊥平面ABCD,底面ABCD是直角梯形,∠ABC=∠BCD=90°,PB=BC=CD=
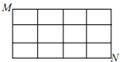 如图,在某个城市中,M,N两地之间有南北街道5条、东西街道4条,现要求沿图中的街道,以最短的路程从M走到N,则不同的走法共有
如图,在某个城市中,M,N两地之间有南北街道5条、东西街道4条,现要求沿图中的街道,以最短的路程从M走到N,则不同的走法共有