题目内容
已知函数f(x)=ex-
x2-ax(a∈R).
(Ⅰ)若函数f(x)的图象在x=0处的切线方程为y=2x+b,求a,b的值;
(Ⅱ)若函数在R上是增函数,求实数a的取值范围.
| 1 |
| 2 |
(Ⅰ)若函数f(x)的图象在x=0处的切线方程为y=2x+b,求a,b的值;
(Ⅱ)若函数在R上是增函数,求实数a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的概念及应用
分析:(Ⅰ)先求出f′(x)=ex-x-a,从而f′(0)=1-a=2,解得:a=-1,得f(x)=ex-
x2+x,解得:b=1.
(Ⅱ)由题意f′(x)>0,即ex-x-a≥0恒成立,得a≤ex-x恒成立,设h(x)=ex-x,求出h(x)min=h(0)=1,从而a≤1.
| 1 |
| 2 |
(Ⅱ)由题意f′(x)>0,即ex-x-a≥0恒成立,得a≤ex-x恒成立,设h(x)=ex-x,求出h(x)min=h(0)=1,从而a≤1.
解答:
解:(Ⅰ)∵f′(x)=ex-x-a,
∴f′(0)=1-a=2,解得:a=-1,
∴f(x)=ex-
x2+x,
∴f(0)=1,
∴1=2×0+b,解得:b=1.
(Ⅱ)由题意f′(x)>0,即ex-x-a≥0恒成立,
∴a≤ex-x恒成立,
设h(x)=ex-x,则h′(x)=ex-1,
令h′(x)>0,解得:x>0,
令h′(x)<0,解得:x<0,
∴h(x)在(-∞,0)递减,在(0,+∞)递增,
∴h(x)min=h(0)=1,
∴a≤1.
∴f′(0)=1-a=2,解得:a=-1,
∴f(x)=ex-
| 1 |
| 2 |
∴f(0)=1,
∴1=2×0+b,解得:b=1.
(Ⅱ)由题意f′(x)>0,即ex-x-a≥0恒成立,
∴a≤ex-x恒成立,
设h(x)=ex-x,则h′(x)=ex-1,
令h′(x)>0,解得:x>0,
令h′(x)<0,解得:x<0,
∴h(x)在(-∞,0)递减,在(0,+∞)递增,
∴h(x)min=h(0)=1,
∴a≤1.
点评:本题考察了函数的单调性,导数的应用,求参数的范围,是一道基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
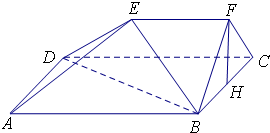 如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=
如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=