题目内容
求函数f(x)=
sinx+cosx,x∈[0,π]的值域.
| 2 |
考点:两角和与差的正弦函数,函数的值域
专题:三角函数的求值
分析:先把函数表示成f(x)=
sin(x+α)的形式,再用正弦函数的性质求出值域.
| 3 |
解答:
解:f(x)=
sinx+cosx
=
(
sinx+
cosx)
=
sin(x+α),(其中sinα=
)
∵x∈[0,π],∴x+α∈[α,π+α],
由正弦函数的性质得,
当x+α=
,即x=
-α时,f(x)max=
,
当x+α=π+α时f(x)min=
sin(π+α)=-
sinα=-
×
=-1;
∴函数f(x)=
sinx+cosx,x∈[0,π]的值域为[-1,
].
| 2 |
=
| 3 |
| ||
| 3 |
| ||
| 3 |
=
| 3 |
| ||
| 3 |
∵x∈[0,π],∴x+α∈[α,π+α],
由正弦函数的性质得,
当x+α=
| π |
| 2 |
| π |
| 2 |
| 3 |
当x+α=π+α时f(x)min=
| 3 |
| 3 |
| 3 |
| ||
| 3 |
∴函数f(x)=
| 2 |
| 3 |
点评:本题考察了求三角函数的值域问题,解题时一定要注意自变量的取值,以免出错.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
(理)要从10名女生和5名男生中选出6名学生组成课外兴趣小组学习,则按分层抽样组成此课外兴趣小组的概率为( )
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知z(1+2i)=4+3i,则|z|=( )
A、
| ||
B、
| ||
| C、2 | ||
D、
|
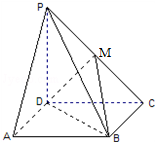 在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.
在四棱锥P-ABCD中,侧棱PD⊥底面ABCD,底面ABCD是正方形,若PD=DA,M是PC的中点.