题目内容
已知椭圆E的两个焦点分别为(-1,0)和(1,0),离心率e=
.
(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线l:y=x+m(m≠0)与椭圆E交于A、B两点,线段AB的垂直平分线交x轴于点T,当m变化时,求△TAB面积的最大值.
| ||
| 2 |
(Ⅰ)求椭圆E的方程;
(Ⅱ)设直线l:y=x+m(m≠0)与椭圆E交于A、B两点,线段AB的垂直平分线交x轴于点T,当m变化时,求△TAB面积的最大值.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据椭圆的焦点坐标,离心率,求出a,c,可求b,即可求椭圆E的方程;
(Ⅱ)直线y=x+m代入椭圆方程,求出|AB|,|MT|,可得△TAB的面积,配方,即可求出三角形面积的最大值.
(Ⅱ)直线y=x+m代入椭圆方程,求出|AB|,|MT|,可得△TAB的面积,配方,即可求出三角形面积的最大值.
解答:
解:(Ⅰ)由已知椭圆的焦点在x轴上,c=1,
=
,
∴a=
,b=1,---(2分)
∴椭圆E的方程为
+y2=1---(4分)
(Ⅱ)y=x+m代入椭圆方程,消去y得3x2+4mx+2m2-2=0
∵直线l与椭圆有两个交点,
∴△>0,可得m2<3(*)---(6分)
设A(x1,y1),B(x2,y2),
∴x1+x2=-
,x1x2=
,
∴弦长|AB|=
|x1-x2|=
•
,---(8分)
AB中点M(-
,
),设T(x,0),∴kAB•kMT=-1,
∴
•1=-1,
∴x=-
,
∴T(-
,0),|TM|=
---(11分)
∴S=
|AB||MT|=
∵m2<3,∴m2=
时,Smax=
--(14分)
| c |
| a |
| ||
| 2 |
∴a=
| 2 |
∴椭圆E的方程为
| x2 |
| 2 |
(Ⅱ)y=x+m代入椭圆方程,消去y得3x2+4mx+2m2-2=0
∵直线l与椭圆有两个交点,
∴△>0,可得m2<3(*)---(6分)
设A(x1,y1),B(x2,y2),
∴x1+x2=-
| 4m |
| 3 |
| 2m2-2 |
| 3 |
∴弦长|AB|=
| 2 |
2
| ||
| 3 |
| 6-2m2 |
AB中点M(-
| 2m |
| 3 |
| m |
| 3 |
∴
| ||
-
|
∴x=-
| m |
| 3 |
∴T(-
| m |
| 3 |
| ||
| 3 |
∴S=
| 1 |
| 2 |
| 2 |
| 9 |
-2(m2-
|
∵m2<3,∴m2=
| 3 |
| 2 |
| ||
| 3 |
点评:待定系数法是解决椭圆标准方程的关键,直线与圆锥曲线联立,是解决弦长问题的常用方法.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
在如图的程序中所有的输出结果之和为( )


| A、30 | B、16 | C、14 | D、9 |
已知命题p:函数f(x)=|sin
x|的最小正周期是π;命题q:若函数f(x-1)是奇函数,则f(x)的图象关于点(-1,0)对称,下列命题是真命题的是( )
| 1 |
| 2 |
| A、p∧q |
| B、p∨q |
| C、(¬p)∧(¬q) |
| D、p∨(¬q) |
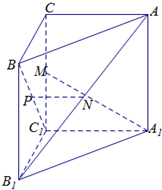 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,且∠ACB=90°,∠BAC=30°,BC=1,AA1=