题目内容
在（0，2π）内，使|sinx|≥cosx成立的x的取值范围为（ ）
A、[
| ||||
B、[
| ||||
C、[0，
| ||||
D、[0，
|
考点：三角不等式
专题：三角函数的图像与性质
分析：由x在（0，2π）范围内，在平面直角坐标系中画出y=|sinx|和y=cosx的图象，根据图象可知在图中阴影部分取x的值写出满足题意x的范围即可．
解答：
解：在（0，2π）内，画出y=|sinx|及y=cosx的图象，
由函数的图象可知，阴影部分的|sinx|≥cosx，
则满足题意的x的取值范围为[
，
]．
故选A．
由函数的图象可知，阴影部分的|sinx|≥cosx，
则满足题意的x的取值范围为[
| π |
| 4 |
| 7π |
| 4 |
故选A．
点评：此题考查学生灵活运用同角三角函数间的基本关系化简求值，掌握正弦、余弦函数的图象与性质，考查了数形结合的数学思想．
练习册系列答案
相关题目
已知函数f（x）的导函数为f′（x），且满足f′（x）＜2f（x），则（ ）
| A、f（2）＞e2f（1） |
| B、e2f（0）＞f（1） |
| C、9f（ln2）＜4f（ln3） |
| D、e2f（ln2）＜4f（1） |
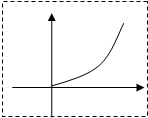已知定义在[0，1]上的函数y=f（x）图象如图所示，且f（1）=1，则对满足0＜x1＜x2＜1的任意x1，x2，下列关系：（1）f（x1）＜x1，（2）x1+f（x2）＜x2+f（x1），（3）x2f（x1）＜x1f（x2）其中一定正确的是