题目内容
已知等差数列{an}的前n项和为Sn,且a3+a9=3a6-4,则S11= .
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由等差数列的性质和已知可得a6=4,再由求和公式和性质可得S11=11a6,代值计算可得.
解答:
解:由等差数列的性质可得a3+a9=2a6,
又a3+a9=3a6-4,∴2a6=3a6-4,
解得a6=4,
∴S11=
=
=11a6=44
故答案为:44
又a3+a9=3a6-4,∴2a6=3a6-4,
解得a6=4,
∴S11=
| 11(a1+a11) |
| 2 |
| 11×2a6 |
| 2 |
故答案为:44
点评:本题考查等差数列的前n项和公式和等差数列的性质,属基础题.

练习册系列答案
相关题目
已知集合A={x|y=lg(2x-x2)},B={y|y=2x,x>0},R是实数集,则(∁RB)∩A=( )
| A、(0,1] |
| B、[0,1] |
| C、(-∞,0] |
| D、以上都不对 |
已知{1,2,3},B={2,4},定义A-B={x|x∈A且x∉B},则A-B=( )
| A、{1,2,3} |
| B、{2,4} |
| C、{1,3} |
| D、{2} |
已知函数f(x)的导函数为f′(x),且满足f′(x)<2f(x),则( )
| A、f(2)>e2f(1) |
| B、e2f(0)>f(1) |
| C、9f(ln2)<4f(ln3) |
| D、e2f(ln2)<4f(1) |
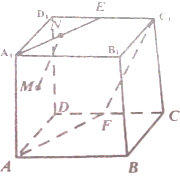 正方体AC1中,E,F分别是D1C1,DC的中点,N是A1E的中点,M为正方形A1ADD1的中心.
正方体AC1中,E,F分别是D1C1,DC的中点,N是A1E的中点,M为正方形A1ADD1的中心.
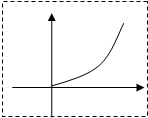 已知定义在[0,1]上的函数y=f(x)图象如图所示,且f(1)=1,则对满足0<x1<x2<1的任意x1,x2,下列关系:(1)f(x1)<x1,(2)x1+f(x2)<x2+f(x1),(3)x2f(x1)<x1f(x2)其中一定正确的是
已知定义在[0,1]上的函数y=f(x)图象如图所示,且f(1)=1,则对满足0<x1<x2<1的任意x1,x2,下列关系:(1)f(x1)<x1,(2)x1+f(x2)<x2+f(x1),(3)x2f(x1)<x1f(x2)其中一定正确的是