题目内容
设数列{bn}满足bn+2=-bn+1-bn(n∈N*),b2=2b1.
(1)若b3=3,求b1的值;
(2)求证数列{bnbn+1bn+2+n}是等差数列;
(3)设数列{Tn}满足:Tn+1=Tnbn+1(n∈N*),且T1=b1=-
,若存在实数p,q,对任意n∈N*都有p≤T1+T2+T3+…+Tn<q成立,试求q-p的最小值.
(1)若b3=3,求b1的值;
(2)求证数列{bnbn+1bn+2+n}是等差数列;
(3)设数列{Tn}满足:Tn+1=Tnbn+1(n∈N*),且T1=b1=-
| 1 |
| 2 |
考点:数列与不等式的综合
专题:综合题,压轴题,等差数列与等比数列,不等式的解法及应用
分析:(1)直接由已知b3=3结合题目给出的数列递推式求b1的值;
(2)由bn+2=-bn+1-bn,bn+3=-bn+2-bn+1,作差后得到bn+3=bn,进一步利用作差法证明数列{bnbn-1bn-2+n}是等差数列;
(3)由Tn+1=Tn•bn+1=Tn-1bnbn+1=Tn-2bn-1bnbn+1=…=b1b2b3…bn+1,得到当n≥2时,Tn=b1b2b2…bn,然后推出数列{T3n-2+T3n-1+T3n)(n∈N*)是等比数列,求出其前n项和Sn=T1+T2+T3+…+Tn,再对n分当n=3k(k∈N*)时,当n=3k-1(k∈N*)时,当n=3k-2(k∈N*)时具体求和,最后利用放缩法得答案.
(2)由bn+2=-bn+1-bn,bn+3=-bn+2-bn+1,作差后得到bn+3=bn,进一步利用作差法证明数列{bnbn-1bn-2+n}是等差数列;
(3)由Tn+1=Tn•bn+1=Tn-1bnbn+1=Tn-2bn-1bnbn+1=…=b1b2b3…bn+1,得到当n≥2时,Tn=b1b2b2…bn,然后推出数列{T3n-2+T3n-1+T3n)(n∈N*)是等比数列,求出其前n项和Sn=T1+T2+T3+…+Tn,再对n分当n=3k(k∈N*)时,当n=3k-1(k∈N*)时,当n=3k-2(k∈N*)时具体求和,最后利用放缩法得答案.
解答:
(1)解:∵bn+2=-bn+1-bn,
∴b3=-b2-b1=-3b1=3,
∴b1=-1;
(2)证明:∵bn+2=-bn+1-bn ①,
∴bn+3=-bn+2-bn+1 ②,
②-①得bn+3=bn,
∴(bn+1bn+2bn+3+n+1)-(bnbn+1bn+2+n)=bn+1bn+2(bn+3-bn)+1=1为常数,
∴数列{bnbn+1bn+2+n}是等差数列;
(3)解:∵Tn+1=Tn•bn+1=Tn-1bnbn+1=Tn-2bn-1bnbn+1=…=b1b2b3…bn+1,
当n≥2时,Tn=b1b2b2…bn(*),
当n=1时,T1=b1适合(*)式
∴Tn=b1b2b3…bn(n∈N*).
∵b1=-
,b2=2b1=-1,
b3=-3b1=
,bn+3=bn,
∴T1=b1=-
,T2=T1b2=
,
T3=T2b3=
,T4=T3b4=T3b1=
T1,
T5=T4b5=T2b3b4b5=T2b1b2b3=
T2,
T6=T5b6=T3b4b5b6=T3b1b2b3=
T3,
…
T3n+1+T3n+2+T3n+3=T3n-2b3n-1b3nb3n+1+
T3n-1b3nb3n+1b3n+2+T3nb3n+1b3n+2b3n+3
=T3n-2b1b2b3+T3n-1b1b2b3+T3nb1b2b3
=
(T3n-2+T3n-1+T3n),
∴数列{T3n-2+T3n-1+T3n)(n∈N*)是等比数列,
首项T1+T2+T3=
且公比q=
,
记Sn=T1+T2+T3+…+Tn,
①当n=3k(k∈N*)时,
Sn=(T1+T2+T3)+(T4+T5+T6)…+(T3k-2+T3k-1+T3k)
=
=3[1-(
)k].
∴
≤Sn<3;
②当n=3k-1(k∈N*)时,
Sn=(T1+T2+T3)+(T4+T5+T6)+…+(T3k-2+T3k-1+T3k)-T3k
=3[1-(
)k]-(b1b2b3)k=3-4•(
)k.
∴0≤Sn<3;
③当n=3k-2(k∈N*)时,
Sn=(T1+T2+T3)+(T4+T5+T6)+…+(T3k-2+T3k-1+T3k)-T3k-1-T3k
=3[1-(
)k]-(b1b2b3)k-1b1b2-(b1b2b3)k
=3[1-(
)k]-
(
)k-1-(
)k
=3-
•(
)k.
∴-
≤Sn<3.
综上得:-
≤Sn<3.
则p≤-
且q≥3.
∴q-p的最小值为
.
∴b3=-b2-b1=-3b1=3,
∴b1=-1;
(2)证明:∵bn+2=-bn+1-bn ①,
∴bn+3=-bn+2-bn+1 ②,
②-①得bn+3=bn,
∴(bn+1bn+2bn+3+n+1)-(bnbn+1bn+2+n)=bn+1bn+2(bn+3-bn)+1=1为常数,
∴数列{bnbn+1bn+2+n}是等差数列;
(3)解:∵Tn+1=Tn•bn+1=Tn-1bnbn+1=Tn-2bn-1bnbn+1=…=b1b2b3…bn+1,
当n≥2时,Tn=b1b2b2…bn(*),
当n=1时,T1=b1适合(*)式
∴Tn=b1b2b3…bn(n∈N*).
∵b1=-
| 1 |
| 2 |
b3=-3b1=
| 3 |
| 2 |
∴T1=b1=-
| 1 |
| 2 |
| 1 |
| 2 |
T3=T2b3=
| 3 |
| 4 |
| 3 |
| 4 |
T5=T4b5=T2b3b4b5=T2b1b2b3=
| 3 |
| 4 |
T6=T5b6=T3b4b5b6=T3b1b2b3=
| 3 |
| 4 |
…
T3n+1+T3n+2+T3n+3=T3n-2b3n-1b3nb3n+1+
T3n-1b3nb3n+1b3n+2+T3nb3n+1b3n+2b3n+3
=T3n-2b1b2b3+T3n-1b1b2b3+T3nb1b2b3
=
| 3 |
| 4 |
∴数列{T3n-2+T3n-1+T3n)(n∈N*)是等比数列,
首项T1+T2+T3=
| 3 |
| 4 |
| 3 |
| 4 |
记Sn=T1+T2+T3+…+Tn,
①当n=3k(k∈N*)时,
Sn=(T1+T2+T3)+(T4+T5+T6)…+(T3k-2+T3k-1+T3k)
=
| ||||
1-
|
| 3 |
| 4 |
∴
| 3 |
| 4 |
②当n=3k-1(k∈N*)时,
Sn=(T1+T2+T3)+(T4+T5+T6)+…+(T3k-2+T3k-1+T3k)-T3k
=3[1-(
| 3 |
| 4 |
| 3 |
| 4 |
∴0≤Sn<3;
③当n=3k-2(k∈N*)时,
Sn=(T1+T2+T3)+(T4+T5+T6)+…+(T3k-2+T3k-1+T3k)-T3k-1-T3k
=3[1-(
| 3 |
| 4 |
=3[1-(
| 3 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
=3-
| 14 |
| 3 |
| 3 |
| 4 |
∴-
| 1 |
| 2 |
综上得:-
| 1 |
| 2 |
则p≤-
| 1 |
| 2 |
∴q-p的最小值为
| 7 |
| 2 |
点评:本题考查了等差关系的判断与应用,考查了等比关系的判断,训练了数列的分组求和与等比数列的前n项和,考查了数列不等式的解法,体现了分类讨论的数学思想方法,是压轴题.

练习册系列答案
相关题目
已知函数f(x)=
,则f(f(5))=( )
|
| A、-1 | B、1 | C、-2 | D、2 |
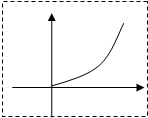 已知定义在[0,1]上的函数y=f(x)图象如图所示,且f(1)=1,则对满足0<x1<x2<1的任意x1,x2,下列关系:(1)f(x1)<x1,(2)x1+f(x2)<x2+f(x1),(3)x2f(x1)<x1f(x2)其中一定正确的是
已知定义在[0,1]上的函数y=f(x)图象如图所示,且f(1)=1,则对满足0<x1<x2<1的任意x1,x2,下列关系:(1)f(x1)<x1,(2)x1+f(x2)<x2+f(x1),(3)x2f(x1)<x1f(x2)其中一定正确的是