题目内容
已知底面边长为
，侧棱长为6的正四棱柱的各顶点均在同一个球面上，其对角线为直径，则该球的体积为（ ）
| 3 |
A、
| ||
B、7
| ||
C、
| ||
D、
|
考点：球的体积和表面积
专题：空间位置关系与距离
分析：由长方体的对角线公式，算出正四棱柱体对角线的长，从而得到球直径长，得球半径R=1，最后根据球的体积公式，可算出此球的体积．
解答：
解：∵正四棱柱的底面边长为
，侧棱长为6，
∴正四棱柱体对角线的长为
=
，
又∵正四棱柱的顶点在同一球面上，
∴正四棱柱体对角线恰好是球的一条直径，得球半径R=
，
根据球的体积公式，得此球的体积为V=
πR3=7
π．
故选：B．
| 3 |
∴正四棱柱体对角线的长为
| 3+3+36 |
| 42 |
又∵正四棱柱的顶点在同一球面上，
∴正四棱柱体对角线恰好是球的一条直径，得球半径R=
| ||
| 2 |
根据球的体积公式，得此球的体积为V=
| 4 |
| 3 |
| 42 |
故选：B．
点评：本题给出球内接正四棱柱的底面边长和侧棱长，求该球的体积，考查了正四棱柱的性质、长方体对角线公式和球的体积公式等知识，属于基础题．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
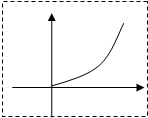已知定义在[0，1]上的函数y=f（x）图象如图所示，且f（1）=1，则对满足0＜x1＜x2＜1的任意x1，x2，下列关系：（1）f（x1）＜x1，（2）x1+f（x2）＜x2+f（x1），（3）x2f（x1）＜x1f（x2）其中一定正确的是
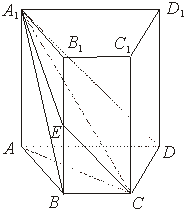如图，四棱柱ABCD-A1B1C1D1中，A1A⊥底面ABCD，且A1A=4．梯形ABCD的面积为6，且AD∥BC，AD=2BC，AB=2．平面A1DCE与B1B交于点E．