Question

5．已知函数f（x）=$\left\{\begin{array}{l}\frac{2}{x}，x＞1\\ 9x{（1-x）^2}，x≤1\end{array}$，若函数g（x）=f（x）-k仅有一个零点，则k的取值范围是（-∞，0）∪（$\frac{4}{3}$，2）．

Answer 1

分析 判断f（x）的单调性，计算f（x）的极值，作出f（x）的函数图象，根据图象即可判断出k的范围．

解答 解：当x＞1时，f（x）单调递减，
当x≤1时，f′（x）=9（3x-1）（x-1），
∴当x$＜\frac{1}{3}$时，f′（x）＞0，当$\frac{1}{3}＜x＜1$时，f′（x）＜0，
∴f（x）在（-∞，$\frac{1}{3}$）上单调递增，在（$\frac{1}{3}$，1）上单调递减，
∴当x=$\frac{1}{3}$时，f（x）取得极大值f（$\frac{1}{3}$）=$\frac{4}{3}$．
作出f（x）的函数图象如图所示：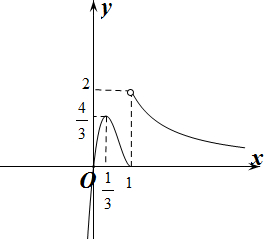

∵函数g（x）=f（x）-k仅有一个零点，
∴k＜0或$\frac{4}{3}＜x＜2$．
故答案为：（-∞，0）∪（$\frac{4}{3}$，2）．

点评 本题考查了函数单调性判断与极值计算，函数零点与函数图象的关系，属于中档题．