题目内容
13.已知Z是复数,|Z-2+i|=$\sqrt{3}$,则|z|的取值范围[$\sqrt{5}-\sqrt{3}$,$\sqrt{5}+\sqrt{3}$].分析 由题意画出图形,求出圆心到原点的距离,数形结合得答案.
解答 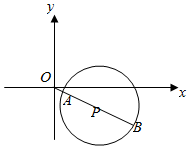 解:|Z-2+i|=$\sqrt{3}$的几何意义为复平面内动点Z到定点P(2,-1)的距离为$\sqrt{3}$的轨迹,
解:|Z-2+i|=$\sqrt{3}$的几何意义为复平面内动点Z到定点P(2,-1)的距离为$\sqrt{3}$的轨迹,
如图:
∵|OP|=$\sqrt{5}$,
∴|z|的最小值为$\sqrt{5}-\sqrt{3}$,最大值为$\sqrt{5}+\sqrt{3}$.
取值范围为[$\sqrt{5}-\sqrt{3}$,$\sqrt{5}+\sqrt{3}$].
故答案为:[$\sqrt{5}-\sqrt{3}$,$\sqrt{5}+\sqrt{3}$].
点评 题考查复数模的求法,考查数形结合的解题思想方法,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.若命题p的逆命题是q,否命题是r,则命题q是命题r的( )
| A. | 逆命题 | B. | 否命题 | C. | 逆否命题 | D. | 不等价命题 |
8.某班有学生55人,现将所有学生按1,2,3,…,55,随机编号,若采用系统抽样的方法抽取一个容量为5的样本,已知编号为6,a,28,b,50的学生在样本中,则a+b=( )
| A. | 52 | B. | 54 | C. | 55 | D. | 56 |
3.(1-x-5y)5的展开式中不含x的项的系数和为( )(结果化成最简形式).
| A. | 1024 | B. | -1024 | C. | 1025 | D. | -1028 |