题目内容
在△ABC中,已知A(-1,5),∠B和∠C的平分线所在直线的方程分别为x-y+2=0和y=2,求△ABC的面积.
考点:正弦定理
专题:解三角形
分析:利用解方程组的方法,根据角平分线的对称性对称A(-1,5)关于x-y+2=0对称点P(x1,y1),A(-1,5)关于y=2对称点Q(x2,y2),求出BC的方程,
结合角平分线方程得出B,C 坐标,最求解|BC|=5
,A点到直线BC的距离为:d=
,利用面积公式求解得出△ABC的面积为
×5
×
=30,
结合角平分线方程得出B,C 坐标,最求解|BC|=5
| 5 |
| 12 | ||
|
| 1 |
| 2 |
| 5 |
| 12 | ||
|
解答:
 解:∵A(-1,5),∠B和∠C的平分线所在直线的方程分别为x-y+2=0和y=2,
解:∵A(-1,5),∠B和∠C的平分线所在直线的方程分别为x-y+2=0和y=2,
∴A(-1,5)关于x-y+2=0对称点P(x1,y1),
解得:x1=3,y1=1,P(3,1),
∵A(-1,5)关于y=2对称点Q(x2,y2),
∴Q(-1,-1)
∵P,Q都在直线BC上,
∴kBC=
,BC的方程为:y=
x-
,
得
,
B(-5,-3),
,C(5,2)
∴|BC|=5
,
A点到直线BC的距离为:d=
,
∴△ABC的面积为
×5
×
=30,
 解:∵A(-1,5),∠B和∠C的平分线所在直线的方程分别为x-y+2=0和y=2,
解:∵A(-1,5),∠B和∠C的平分线所在直线的方程分别为x-y+2=0和y=2,∴A(-1,5)关于x-y+2=0对称点P(x1,y1),
|
∵A(-1,5)关于y=2对称点Q(x2,y2),
∴Q(-1,-1)
∵P,Q都在直线BC上,
∴kBC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
|
|
B(-5,-3),
|
∴|BC|=5
| 5 |
A点到直线BC的距离为:d=
| 12 | ||
|
∴△ABC的面积为
| 1 |
| 2 |
| 5 |
| 12 | ||
|
点评:本题考查了平面直线与点的对称,方程组的运用,属于计算题,结合图形求解,思路简单些.

练习册系列答案
相关题目
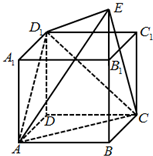 如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,|BB1|=a,E为BB1延长线上的一点且满足|BB1|•|B1E|=1.
如图长方体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形,|BB1|=a,E为BB1延长线上的一点且满足|BB1|•|B1E|=1.