题目内容
已知集合A={x|1＜ax＜2（a≥0）}，B={x|-1＜x＜1}，是否存在实数a满足A⊆B，若存在，求出a的取值范围．
考点：集合的包含关系判断及应用
专题：集合
分析：注意对集合A中参数a的讨论．解出集合A．
解答：
解：①当a=0时，A=Φ，A⊆B；
②当a＞0时，A={x|1＜ax＜2}={x|
＜x＜
}，
则-1≤
且
≤1，解得，a≥2．
故a的取值范围a=0或a≥2．
②当a＞0时，A={x|1＜ax＜2}={x|
| 1 |
| a |
| 2 |
| a |
则-1≤
| 1 |
| a |
| 2 |
| a |
故a的取值范围a=0或a≥2．
点评：本题考查了集合间的关系及分类讨论的思想，属于基础题
练习册系列答案
相关题目
下列集合表示方法正确的是（ ）
| A、{1，3，3} |
| B、{全体实数} |
| C、{2，4} |
| D、不等式x2-1＞2的解集是{x2-1＞0} |
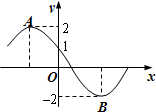如图所示为函数f（x）=2sin（ωx+φ）（ω＞0，
