题目内容
已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为
,则
的值为( )
| 1 |
| 3 |
| AD |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:几何概型
专题:概率与统计
分析:根据概率,确定构成事件M的长度为线段CD的
,根据对称性,当PD=
CD时,AB=PB,利用勾股定理,即可得出结论.
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:记“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”为事件M,试验的全部结果构成的长度即为线段CD,构成事件M的长度为线段CD的
,
设AB=3x,AD=y,则
根据对称性,当PD=
CD时,AB=PB,
由勾股定理可得(3x)2=y2+(2x)2,
∴y=
x,
∴
=
=
.
故选B.
| 1 |
| 3 |
设AB=3x,AD=y,则
根据对称性,当PD=
| 1 |
| 3 |
由勾股定理可得(3x)2=y2+(2x)2,
∴y=
| 5 |
∴
| AD |
| AB |
| y |
| 3x |
| ||
| 3 |
故选B.
点评:本题主要考查几何概型,基本方法是:分别求得构成事件A的区域长度和试验的全部结果所构成的区域长度,两者求比值,即为概率.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
经过两点A(4,2y+1),B(2,-3)的直线的倾斜角为
,则y=( )
| 3π |
| 4 |
| A、-1 | B、0 | C、-3 | D、2 |
曲线y=x-
在点(1,0)处的切线方程为( )
| 1 |
| x |
| A、y=2x-2 |
| B、y=x-1 |
| C、y=0 |
| D、y=-x+1 |
已知集合A={x||x|<3},B={x|x-2≤0},则A∪B等( )
| A、(-∞,3] |
| B、(-∞,3) |
| C、[2,3) |
| D、(-3,2] |
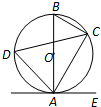 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.