题目内容
两人约定在19:30至20:30之间相见,并且先到者必须等迟到者20分钟方可离去,如果两人出发是各自独立的,在19:30至20:30各时刻相见的可能性是相等的,那么两人在约定时间内相见的概率为 .
考点:几何概型
专题:概率与统计
分析:由题意,试验包含的所有事件是Ω={(x,y)|0<x<1,0<y<1},求出事件对应的集合表示的面积,写出满足条件的事件是A={(x,y)|0<x<1,0<y<1,|x-y|≤
},算出事件对应的集合表示的面积,根据几何概型概率公式得到结果.
| 1 |
| 3 |
解答:
 解:由题意知本题是一个几何概型,设事件A为“甲乙两人能会面”,
解:由题意知本题是一个几何概型,设事件A为“甲乙两人能会面”,
试验包含的所有事件是Ω={(x,y)|0<x<1,0<y<1},并且事件对应的集合表示的面积是S=1,
满足条件的事件是A={(x,y)|0<x<1,0<y<1,|x-y|≤
=
}.
如图所示,两人到达的时刻均匀地分布在一个边长为1的正方形Ⅰ内,而相遇现象则发生在阴影区域G内,
所以两人相遇的概率为区域G与区域Ⅰ的面积之比为
=
.
故答案为:
.
 解:由题意知本题是一个几何概型,设事件A为“甲乙两人能会面”,
解:由题意知本题是一个几何概型,设事件A为“甲乙两人能会面”,试验包含的所有事件是Ω={(x,y)|0<x<1,0<y<1},并且事件对应的集合表示的面积是S=1,
满足条件的事件是A={(x,y)|0<x<1,0<y<1,|x-y|≤
| 20 |
| 60 |
| 1 |
| 3 |
如图所示,两人到达的时刻均匀地分布在一个边长为1的正方形Ⅰ内,而相遇现象则发生在阴影区域G内,
所以两人相遇的概率为区域G与区域Ⅰ的面积之比为
1-(
| ||
| 1 |
| 5 |
| 9 |
故答案为:
| 5 |
| 9 |
点评:解决此类问题的关键是熟练掌握几何概型的定义与概率计算公式,而几何概率模型一般通过事件的长度、面积或者体积之比来求事件发生的概率,属于中档题.

练习册系列答案
相关题目
将直线2x-y+λ=0沿x轴向左平移一个单位,所得直线与曲线C:
(θ为参数)相切,则实数λ的值为( )
|
| A、-7或3 | B、-2或8 |
| C、0或10 | D、1或11 |
已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为
,则
的值为( )
| 1 |
| 3 |
| AD |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
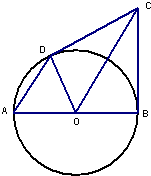 (几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD=
(几何证明选讲选做题)如图,AB是圆O的直径,BC是圆O的切线,切点为B,OC平行于弦AD,若OB=3,OC=5,则CD= 已知函数f(x)=lg(2+x)+lg(2-x).
已知函数f(x)=lg(2+x)+lg(2-x).