题目内容
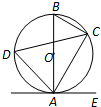 如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
考点:圆的切线的判定定理的证明,圆的切线的性质定理的证明
专题:计算题,证明题,直线与圆
分析:(1)根据∠ABC与∠D都是劣弧AC所对的圆周角,利用圆周角定理可证出∠ABC=∠D=60°;
(2)根据AB是⊙O的直径,利用直径所对的圆周角是直角得到∠ACB=90°,结合∠ABC=60°求得∠BAC=30°,从而推出∠BAE=90°,即OA⊥AE,可得AE是⊙O的切线;
(3)连结OC,证出△OBC是等边三角形,算出∠BOC=60°且⊙O的半径等于4,可得劣弧AC所对的圆心角∠AOC=120°,再由弧长公式加以计算,可得劣弧AC的长.
(2)根据AB是⊙O的直径,利用直径所对的圆周角是直角得到∠ACB=90°,结合∠ABC=60°求得∠BAC=30°,从而推出∠BAE=90°,即OA⊥AE,可得AE是⊙O的切线;
(3)连结OC,证出△OBC是等边三角形,算出∠BOC=60°且⊙O的半径等于4,可得劣弧AC所对的圆心角∠AOC=120°,再由弧长公式加以计算,可得劣弧AC的长.
解答:
解:(1)∵∠ABC与∠D都是劣弧AC所对的圆周角, ∠D=60°,
∠D=60°,
∴∠ABC=∠D=60°;
(2)∵AB是⊙O的直径,∴∠ACB=90°.
可得∠BAC=90°-∠ABC=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,
即BA⊥AE,得OA⊥AE,
又∵OA是⊙O的半径,∴AE是⊙O的切线;
(3)如图,连接OC,
∵∠ABC=60°,OB=OC,
∴△BOC是等边三角形,得∠BOC=60°,⊙O的半径R=OB=AB=4,
由此得到∠AOC=180°-∠BOC=120°,
因此,劣弧AC的长等于
=
=
.
 ∠D=60°,
∠D=60°,∴∠ABC=∠D=60°;
(2)∵AB是⊙O的直径,∴∠ACB=90°.
可得∠BAC=90°-∠ABC=30°,
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,
即BA⊥AE,得OA⊥AE,
又∵OA是⊙O的半径,∴AE是⊙O的切线;
(3)如图,连接OC,
∵∠ABC=60°,OB=OC,
∴△BOC是等边三角形,得∠BOC=60°,⊙O的半径R=OB=AB=4,
由此得到∠AOC=180°-∠BOC=120°,
因此,劣弧AC的长等于
| 120πR |
| 180 |
| 120π•4 |
| 180 |
| 8π |
| 3 |
点评:本题着重考查了切线的判定、圆周角定理以及弧长公式等知识,属于中档题.解题过程中,请注意注意辅助线的作法与数形结合思想的应用.

练习册系列答案
 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
一个三棱柱的侧棱垂直于底面,且所有棱长都为a,则此三棱柱的外接球的表面积为( )
| A、πa2 | ||
| B、15πa2 | ||
C、
| ||
D、
|
将直线2x-y+λ=0沿x轴向左平移一个单位,所得直线与曲线C:
(θ为参数)相切,则实数λ的值为( )
|
| A、-7或3 | B、-2或8 |
| C、0或10 | D、1或11 |
已知事件“在矩形ABCD的边CD上随机取一点P,使△APB的最大边是AB”发生的概率为
,则
的值为( )
| 1 |
| 3 |
| AD |
| AB |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
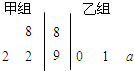 如图所示茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.
如图所示茎叶图记录了甲、乙两组各三名同学在期末考试中的数学成绩.乙组记录中有一个数字模糊,无法确认,假设这个数字具有随机性,并在图中以a表示.