题目内容
已知函数f(x)=x2+2ax+3,x∈[-4,6].
(1)当a=-2时,求f(x)的最值;
(2)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
(3)当a=1时,求f(|x|)的单调区间.
[解析] (1)a=-2时,f(x)=x2-4x+3=(x-2)2-1,
∵x∈[-4,6],∴f(x)min=f(2)=-1,f(x)max=f(-4)=35.
(2)f(x)=x2+2ax+3=(x+a)2+3-a2,
要使f(x)在[-4,6]上是单调函数,
应有-a≤-4或-a≥6,∴a≥4或a≤-6.
(3)a=1时,f(x)=x2+2x+3=(x+1)2+2,f(|x|)=(|x|+1)2+2.
令t=|x|(-4≤x≤6),则0≤t≤6,
∵t=|x|在[-4,0]上单调递减,在[0,6]上单调递增,y=(t+1)2+2在[0,6]上单调递增,
∴f(|x|)在[-4,0]上单调递减,在[0,6]上单调递增.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
某公司欲投资13亿元进行项目开发,现有以下6个项目可供选择.
| 项目 | A | B | C | D | E | F |
| 投资额(亿元) | 5 | 2 | 6 | 4 | 6 | 1 |
| 利润(亿元) | 0.55 | 0.4 | 0.6 | 0.5 | 0.9 | 0.1 |
设计一个投资方案,使投资13亿元所获利润大于1.6亿元,则应选的项目是________(只需写出项目的代号).
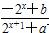 是奇函数.
是奇函数.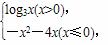 此函数的“友好点对”有( )
此函数的“友好点对”有( )