题目内容
一条光线从点A（-2，3）射出，经x轴反射后，反射光线经过点B（3，2），则反射光线所在的直线方程为 ．
考点：与直线关于点、直线对称的直线方程
专题：直线与圆
分析：设点A（-2，3）关于x轴的对称点为A′（-2，-3），作出图形，依题意知，A′（-2，-3）在反射光线上，反射光线经过点B（3，2），从而可求反射光线所在的直线方程．
解答：
解：设点A（-2，3）关于x轴的对称点为A′（-2，-3），
依题意知，A′（-2，-3）在反射光线上，反射光线经过点B（3，2），
∴反射光线l的斜率k=
=1，l经过点B（3，2），由点斜式得发射光线l的方程为：y-2=x-3，
整理得：y=x-1．
故答案为：y=x-1．
依题意知，A′（-2，-3）在反射光线上，反射光线经过点B（3，2），
∴反射光线l的斜率k=
| 2-(-3) |
| 3-(-2) |
整理得：y=x-1．
故答案为：y=x-1．
点评：本题考查与直线关于点、直线对称的直线方程，分析得到点A（-2，3）关于x轴的对称点为A′（-2，-3）在反射光线上是关键，考查作图能力与运算能力，属于中档题．
练习册系列答案
同步练习强化拓展系列答案
相关题目
在△ABC中，根据下列条件解三角形，其中有两个解的是（ ）
| A、b=10，A=45°，C=60° |
| B、a=6，c=5，B=60° |
| C、a=7，b=5，A=60° |
| D、a=14，b=16，A=45° |
已知f（x）=（ax+2）6，f′（x）是f（x）的导数，若f′（x）的展开式中x的系数大于f（x）的展开式中x的系数，则a的取值范围是（ ）
A、a＞
| ||
B、0＜a＜
| ||
C、a＞
| ||
D、a＞
|
设f0（x）=cosx，且对任意的n∈N，都有 fn+1（x）=fn′（x），则f2013（x）=（ ）
| A、cosx | B、sinx |
| C、-sinx | D、-cosx |
已知数列{an}满足 a1=1，an=1+
，则 a5=（ ）
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
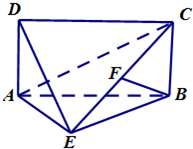如图，四棱锥E-ABCD中，ABCD是矩形，平面EAB⊥平面ABCD，AE=EB=BC=2，F为CE上的点，且BF⊥平面ACE．