Question

16．已知F₁，F₂分别为双曲线E：$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$（a＞0，b＞0）的左、右焦点，离心率为$\frac{5}{3}$，过原点的l交双曲线左、右两支分别于A，B，若|BF₁|-|AF₁|=6，则该双曲线的标准方程为（　　）

• A． $\frac{x^2}{9}-\frac{y^2}{16}=1$
• B． $\frac{x^2}{18}-\frac{y^2}{32}=1$
• C． $\frac{x^2}{9}-\frac{y^2}{25}=1$
• D． $\frac{x^2}{36}-\frac{y^2}{64}=1$

Answer 1

分析 根据题意，作出图形，由双曲线的几何性质分析可得|BF₂|=|AF₁|，结合题意可得|BF₁|-|BF₂|=6，由双曲线的定义分析可得a=3，结合双曲线的离心率可得c的值，进而计算可得b的值，将a、b的值代入双曲线的方程计算可得答案．

解答 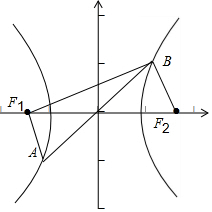解：根据题意，如图F₁，F₂分别为双曲线E的焦点，直线l交双曲线左、右两支分别于A，B，
直线l过原点，则直线l关于原点对称，则有|BF₂|=|AF₁|，
若|BF₁|-|AF₁|=6，则有|BF₁|-|BF₂|=6，
则双曲线E中，2a=6，即a=3，
又由双曲线E的离心率为$\frac{5}{3}$，即e=$\frac{c}{a}$=$\frac{5}{3}$，
则c=5，
b²=c²-a²=25-9=16；
则双曲线的方程为：$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1；
故选：A．

点评 本题考查双曲线的几何性质，关键是利用双曲线的对称性将|BF₁|-|AF₁|=6转化求出a的值．