题目内容
8.已知a,b为正实数,且$\frac{1}{a}$+$\frac{2}{b}$=2,若a+b≥c对满足条件的a,b恒成立,则c的取值范围是( )| A. | (-∞,$\frac{3}{2}$+$\sqrt{2}$] | B. | (-∞,3] | C. | (-∞,6] | D. | (-∞,3+2$\sqrt{2}$] |
分析 利用“乘1法”与基本不等式的性质可得a+b的最小值,即可得出.
解答 解:∵a,b为正实数,且$\frac{1}{a}$+$\frac{2}{b}$=2,
∴a+b=$\frac{1}{2}(\frac{1}{a}+\frac{2}{b})$(a+b)=$\frac{1}{2}$$(3+\frac{2a}{b}+\frac{b}{a})$≥$\frac{1}{2}(3+2\sqrt{\frac{2a}{b}•\frac{b}{a}})$=$\frac{3+2\sqrt{2}}{2}$,当且仅当b=$\sqrt{2}$a=$\frac{2+\sqrt{2}}{2}$时取等号.
∵a+b≥c对满足条件的a,b恒成立,
则c≤$\frac{3}{2}$+$\sqrt{2}$.
故选:A.
点评 本题考查了基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
20. 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
 已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )
已知函数f(x)=x3+bx2+cx+d的图象如图,则函数y=log2(x2+$\frac{2}{3}$bx+$\frac{c}{3}$)的单调递减区间是( )| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
16.已知F1,F2分别为双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的左、右焦点,离心率为$\frac{5}{3}$,过原点的l交双曲线左、右两支分别于A,B,若|BF1|-|AF1|=6,则该双曲线的标准方程为( )
| A. | $\frac{x^2}{9}-\frac{y^2}{16}=1$ | B. | $\frac{x^2}{18}-\frac{y^2}{32}=1$ | C. | $\frac{x^2}{9}-\frac{y^2}{25}=1$ | D. | $\frac{x^2}{36}-\frac{y^2}{64}=1$ |
13.已知向量$\overrightarrow a=(1,\sqrt{1+sin{{40}^0}}),\overrightarrow b=(\frac{1}{{sin{{65}^0}}},x)$共线,则实数x的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}tan{25°}$ | D. | $\sqrt{3}$ |
20.设an=$\frac{1}{n}$+$\frac{1}{n+1}$+$\frac{1}{n+2}$+$\frac{1}{n+3}$+…+$\frac{1}{{n}^{2}}$(n∈N*),则a2=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}$+$\frac{1}{3}$ | C. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$ | D. | $\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$+$\frac{1}{5}$ |
15.现有1名女教师和2名男教师参加说题比赛,共有2道备选题目,若每位选手从中有放回地随机选出一道题进行说题,其中恰有一男一女抽到同一道题的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
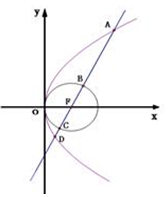 圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点
圆F:(x-1)2-y2=1和抛物线y2=4x,过F的直线l与抛物线和圆依次交于A、B、C、D四点