题目内容
设函数f(x)=
.
(Ⅰ)求f(x)的单调区间;
(Ⅱ)证明;当a≥
时,对任何x≥0,都有f(x)≤ax.
| sinx |
| 2+cosx |
(Ⅰ)求f(x)的单调区间;
(Ⅱ)证明;当a≥
| 1 |
| 3 |
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)先求出函数的导数,从而得出函数的单调区间;(Ⅱ)令g(x)=ax-f(x),求出g(x)的导数,故当a≥
时,g'(x)≥0,进而问题得证.
| 1 |
| 3 |
解答:
解(Ⅰ)f′(x)=
=
.
当2kπ-
<x<2kπ+
(k∈Z)时,cosx>-
,即f'(x)>0;
当2kπ+
<x<2kπ+
(k∈Z)时,cosx<-
,即f'(x)<0.
因此f(x)在每一个区间(2kπ-
,2kπ+
)(k∈Z)是增函数,
f(x)在每一个区间(2kπ+
,2kπ+
)(k∈Z)是减函数.
(Ⅱ)令g(x)=ax-f(x),
则g′(x)=a-
=a-
+
=3(
-
)2+a-
.
故当a≥
时,g'(x)≥0.
又g(0)=0,所以当x≥0时,g(x)≥g(0)=0,
即f(x)≤ax.
| (2+cosx)cosx-sinx(-sinx) |
| (2+cosx)2 |
| 2cosx+1 |
| (2+cosx)2 |
当2kπ-
| 2π |
| 3 |
| 2π |
| 3 |
| 1 |
| 2 |
当2kπ+
| 2π |
| 3 |
| 4π |
| 3 |
| 1 |
| 2 |
因此f(x)在每一个区间(2kπ-
| 2π |
| 3 |
| 2π |
| 3 |
f(x)在每一个区间(2kπ+
| 2π |
| 3 |
| 4π |
| 3 |
(Ⅱ)令g(x)=ax-f(x),
则g′(x)=a-
| 2cosx+1 |
| (2+cosx)2 |
=a-
| 2 |
| 2+cosx |
| 3 |
| (2+cosx)2 |
=3(
| 1 |
| 2+cosx |
| 1 |
| 3 |
| 1 |
| 3 |
故当a≥
| 1 |
| 3 |
又g(0)=0,所以当x≥0时,g(x)≥g(0)=0,
即f(x)≤ax.
点评:本题考查了函数的单调性,导数的应用,考查不等式的证明,是一道中档题.

练习册系列答案
相关题目
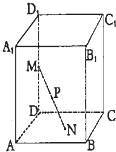 已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为( )
已知直平行六面体ABCD-A1B1C1D1的各条棱长均为3,∠BAD=60°长为2的线段MN的一个端点M在DD1上运动,另一个端点N在底面ABCD上运动,则MN的中点P的轨迹(曲面)与共一顶点D的三个面所围成的几何体的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
有穷数列1,23,26,29,…,23n+6的项数是( )
| A、3n+7 | B、3n+6 |
| C、n+3 | D、n+2 |
已知f(x)=x3+x2f′(1),则f′(2)=( )
| A、0 | B、1 | C、2 | D、3 |
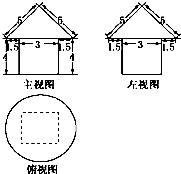 如图是一建筑物的三视图及其尺寸(单位:m),建筑师要在此建筑物的外壁用油漆刷一遍,若每平方米需用油漆0.2kg,则共用的油漆为( )(π取3.14,结果精确到0.01kg)
如图是一建筑物的三视图及其尺寸(单位:m),建筑师要在此建筑物的外壁用油漆刷一遍,若每平方米需用油漆0.2kg,则共用的油漆为( )(π取3.14,结果精确到0.01kg)| A、22.87 kg |
| B、24.67 kg |
| C、26.47 kg |
| D、28.27 kg |
