题目内容
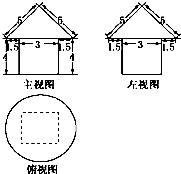如图是一建筑物的三视图及其尺寸（单位：m），建筑师要在此建筑物的外壁用油漆刷一遍，若每平方米需用油漆0.2kg，则共用的油漆为（ ）（π取3.14，结果精确到0.01kg）| A、22.87 kg |
| B、24.67 kg |
| C、26.47 kg |
| D、28.27 kg |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：由题设条件知，此建筑物上部是一个圆锥，下部是一个棱柱，故可求出圆柱的侧面积以及圆锥的侧面积以及圆锥的底面积，用这些的和减去圆柱的上底面积即可求得此建筑物的表面积，再乘以每平方米需用油漆0.2kg则可算出共用的油漆量．
解答：
解：由题设此建筑物上部是以点底面半径为3、母线长为5的一个圆锥，下部是一个高为4、底面边长为3的正四棱柱，
其表面积包括棱柱的侧面积与圆锥的侧面积与圆锥底面的一部分，
棱柱的侧面积为4×4×3=48m2，
圆锥的侧面积为
×2×π×3×5=15πm2，
圆锥的底面积为π×32=9π，
棱柱的底面积为9，
故此建筑物的表面积为48+15π+9π-9=（24π+39）m2，
由于每平方米需用油漆0.2kg油漆，故粉刷这个建筑物的表面积应该用的油漆量为：（24π+39）×0.2≈22.87KG
故选：A．
其表面积包括棱柱的侧面积与圆锥的侧面积与圆锥底面的一部分，
棱柱的侧面积为4×4×3=48m2，
圆锥的侧面积为
| 1 |
| 2 |
圆锥的底面积为π×32=9π，
棱柱的底面积为9，
故此建筑物的表面积为48+15π+9π-9=（24π+39）m2，
由于每平方米需用油漆0.2kg油漆，故粉刷这个建筑物的表面积应该用的油漆量为：（24π+39）×0.2≈22.87KG
故选：A．
点评：本题是基础题，考查几何体的三视图，几何体的表面积和体积的求法，准确判断几何体的形状是解题的关键．
练习册系列答案
相关题目
已知函数f（x）=
，若对于任意x∈R，不等式f（x）≤
-t+1恒成立，则实数t的取值范围是（ ）
|
| t2 |
| 4 |
| A、（-∞，1]∪[2，+∞） |
| B、（-∞，1]∪[3，+∞） |
| C、[1，3] |
| D、（-∞，2]∪[3，+∞） |
计算2sin14°•cos31°+sin17°等于（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
一个几何体的三视图及长度数据如图，则该几何体的表面积为（ ）
| A、8 | ||
B、6+
| ||
C、7+
| ||
D、8+
|
已知直线l经过点（2，
），其横截距与纵截距分别为a，b（a，b均为正数），则使a+b≥c恒成立的c的取值范围（ ）
| 1 |
| 2 |
A、（-∞，
| ||
| B、（0，1] | ||
| C、（-∞，9） | ||
| D、（-∞，8] |
推理“①正方形是平行四边形；②梯形不是平行四边形；③所以梯形不是正方形”中的小前提是（ ）
| A、① | B、② | C、③ | D、①和② |
假设每一架飞机的引擎在飞行中出现故障率为1-p，且各引擎是否有故障是独立的，如有至少50%的引擎能正常运行，飞机就可成功飞行，若使4引擎飞机比2引擎飞机更为安全，则p的取值范围是（ ）
A、（
| ||
B、（
| ||
C、（0，
| ||
D、（0，
|