题目内容
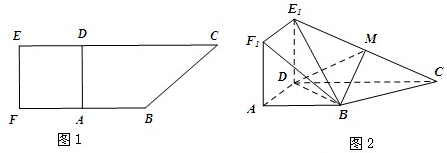
如图1,直角梯形FBCE中,四边形ADEF是正方形,AB=AD=2,CD=4.将正方形沿AD折起,得到如图2所示的多面体,其中面ADE1F1⊥面ABCD,M是E1C中点.
(1)证明:BM∥平面ADE1F1;
(2)求三棱锥D-BME1的体积.
(1)证明:BM∥平面ADE1F1;
(2)求三棱锥D-BME1的体积.

考点:棱柱、棱锥、棱台的体积,直线与平面垂直的判定
专题:空间位置关系与距离
分析:(1)取DE中点N,连结MN,AN.根据三角形中位定理及已知可得MN∥AB,且MN=AB,即四边形ABMN为平行四边形,故BM∥AN,由线面平行的判定定理可得BM∥平面ADE1F1;
(2)由面面垂直的性质定理可得E1D⊥面ABCD,进而E1D⊥BC,利用勾股定理可得BC⊥BD,结合线面垂直的判定定理可得BC⊥平面BDE1,进而由面面垂直的判定定理得到平面BCE1⊥平面BDE1,作DG⊥BE1,则DG⊥平面BCE1,DG是所求三棱锥的高,代入棱锥体积公式可得答案.
(2)由面面垂直的性质定理可得E1D⊥面ABCD,进而E1D⊥BC,利用勾股定理可得BC⊥BD,结合线面垂直的判定定理可得BC⊥平面BDE1,进而由面面垂直的判定定理得到平面BCE1⊥平面BDE1,作DG⊥BE1,则DG⊥平面BCE1,DG是所求三棱锥的高,代入棱锥体积公式可得答案.
解答:
证明: (1)取DE中点N,连结MN,AN.
(1)取DE中点N,连结MN,AN.
在△EDC中,M,N分别为E1C,E1D的中点,
∴MN∥CD,MN=
CD.
由已知AB∥CD,AB=
CD,
∴MN∥AB,且MN=AB.
∴四边形ABMN为平行四边形,
∴BM∥AN.…(3分)
又∵AN?平面ADE1F1,且BM?平面ADE1F1,
∴BM∥平面ADE1F1.…(4分)
解:(2)面ADE1F1⊥面ABCD,E1D?面ADE1F1,面ADE1F1∩面ABCD=AD,E1D⊥AD,
∴E1D⊥面ABCD
又∵BC?面ABCD,
∴E1D⊥BC…(6分)
梯形ABCD中,AB=AD=2,CD=4,∠A=90°,BC=BD=2
∴BD2+BC2=CD2,
∴∠CDB=90°,即BC⊥BD
又∵BD∩E1D=D,
∴BC⊥平面BDE1…(8分)
又BC?平面BCE1,
∴平面BCE1⊥平面BDE1,
作DG⊥BE1,则DG⊥平面BCE1,即DG是所求三棱锥高…(10分)
三棱锥D-BME1的体积V=
•DG•S△BME1=
•DG•S△BCE1,
在直角三角形BDE1中,由面积关系可得DG=
,又S△BCE1=2
∴V=
…(14分)
 (1)取DE中点N,连结MN,AN.
(1)取DE中点N,连结MN,AN.在△EDC中,M,N分别为E1C,E1D的中点,
∴MN∥CD,MN=
| 1 |
| 2 |
由已知AB∥CD,AB=
| 1 |
| 2 |
∴MN∥AB,且MN=AB.
∴四边形ABMN为平行四边形,
∴BM∥AN.…(3分)
又∵AN?平面ADE1F1,且BM?平面ADE1F1,
∴BM∥平面ADE1F1.…(4分)
解:(2)面ADE1F1⊥面ABCD,E1D?面ADE1F1,面ADE1F1∩面ABCD=AD,E1D⊥AD,
∴E1D⊥面ABCD
又∵BC?面ABCD,
∴E1D⊥BC…(6分)
梯形ABCD中,AB=AD=2,CD=4,∠A=90°,BC=BD=2
| 2 |
∴BD2+BC2=CD2,
∴∠CDB=90°,即BC⊥BD
又∵BD∩E1D=D,
∴BC⊥平面BDE1…(8分)
又BC?平面BCE1,
∴平面BCE1⊥平面BDE1,
作DG⊥BE1,则DG⊥平面BCE1,即DG是所求三棱锥高…(10分)
三棱锥D-BME1的体积V=
| 1 |
| 3 |
| 1 |
| 6 |
在直角三角形BDE1中,由面积关系可得DG=
2
| ||
| 3 |
| 6 |
∴V=
| 4 |
| 3 |
点评:本题考查的知识点是棱锥的体积,直线与平面垂直的判定,平面与平面垂直的判定与性质,难度中档.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
经过抛物线y=
x2的焦点和双曲线
-
=1的右焦点的直线方程为( )
| 1 |
| 4 |
| x2 |
| 17 |
| y2 |
| 8 |
| A、x+48y-3=0 |
| B、x+80y-5=0 |
| C、x+3y-3=0 |
| D、x+5y-5=0 |
直线y=5,与y=-1在区间[0,
]上截曲线y=Asinωx+B(A>0,B>0,ω>0)所得弦长相等且不为零,则下列描述正确的是( )
| 2π |
| ω |
A、A≤
| ||||
| B、A≤3,B=2 | ||||
C、A>
| ||||
| D、A>3,B=2 |
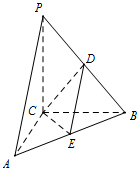 如图,在三棱锥P-ABC中,PB⊥AC,PC⊥平面ABC,点D,E分别为线段PB,AB的中点.
如图,在三棱锥P-ABC中,PB⊥AC,PC⊥平面ABC,点D,E分别为线段PB,AB的中点.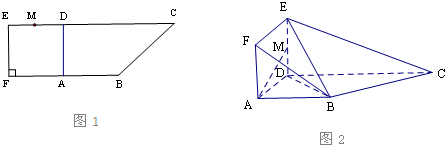
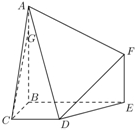 如图,多面体ABCDEF中,BA、BC、BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.
如图,多面体ABCDEF中,BA、BC、BE两两垂直,且AB∥EF,CD∥BE,AB=BE=2,BC=CD=EF=1.