题目内容
规定一种运算“*“：对于任意实数x，y恒有x*x=0，x*（y*z）=（x*y）+z（“+”表示加号），则2013*2014= ．
考点：进行简单的合情推理
专题：推理和证明
分析：本题可以先由定义x*x=0，得到n*n=0，再由x*（y*z）=（x*y）+z推导出n*0=n，然后通过2013*（2014*2014）的分解运算，得到2013*2014=-1，得到本题结论．
解答：
解：∵对于任意实数x，y恒有x*x=0，x*（y*z）=（x*y）+z，
∴n*n=0，
n*（n*n）=（n*n）+n，
∴n*0=0+n=n，
∴2013*（2014*2014）=2013*2014+2014，
即2013*0=2013*2014+2014，
∴2013=2013*2014+2014，
∴2013*2014=-1．
故答案为：-1．
∴n*n=0，
n*（n*n）=（n*n）+n，
∴n*0=0+n=n，
∴2013*（2014*2014）=2013*2014+2014，
即2013*0=2013*2014+2014，
∴2013=2013*2014+2014，
∴2013*2014=-1．
故答案为：-1．
点评：本题考查了新定义运算的知识，解题的关键在于充分理解题意，运用代数思想进行运算，得到本题结论，本题难度适中，有一定的新颖性，属于中档题．
练习册系列答案
相关题目
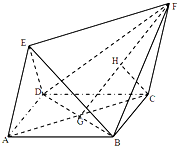如图，四边形ABCD为菱形，ACFE为平行四边形，且面ACFE⊥面ABCD，AB=BD=2，AE=