题目内容
已知f（x+2）=-f（x），求函数周期．
考点：函数的周期性
专题：函数的性质及应用
分析：由已知中f（x+2）=-f（x），可得f（x+4）=-f[（x+2）+2]=-f（x+2）=f（x），进而根据函数周期性的定义，得到T=4．
解答：
解：∵f（x+2）=-f（x），
∴f（x+4）=-f[（x+2）+2]=-f（x+2）=f（x），
∴函数f（x）是以4为周期的周期函数．
∴f（x+4）=-f[（x+2）+2]=-f（x+2）=f（x），
∴函数f（x）是以4为周期的周期函数．
点评：本题考查的知识点是函数的周期性，其中根据已知求出f（x+4）=f（x）是解答的关键．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
已知全集为R，集合A={x|x≤0}，B={x|-1＜x＜2}，则A∩B=（ ）
| A、{x|x≤0} |
| B、{x|-1＜x≤0} |
| C、{x|0≤x＜2} |
| D、∅ |
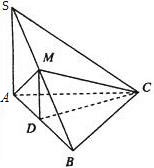如图所示，三棱锥S-ABC中，SA⊥AC，AC⊥BC，M为SB的中点，D为AB的中点，且△AMB为正三角形．