题目内容
20.已知命题p:$?x∈({0,\frac{π}{2}}),sinx-x<0$,命题q:$?{x_0}∈({0,+∞}),{2^{x_0}}=\frac{1}{2}$,则下列命题为真命题的是( )| A. | p∧q | B. | (¬p)∧(-q) | C. | p∧(¬q) | D. | (¬p)∧q |
分析 利用导数研究函数的单调性可得命题p的真假,利用指数函数的单调性即可判断出命题q的真假,再利用复合命题真假的判定方法即可得出.
解答 解:对于命题p.记f(x)=sinx-x.由f'(x)=cosx-1≤0.可知f(x)是定义域上的减函数.则$x∈({0,\frac{π}{2}})$时,f(x)≤f(0)=0,即sinx-x<0,所以命题p是真命题.
对于命题q,当x0>0时,${2^{x_0}}>1$,所以命题q是假命题.
于是p∧(-q)为真命题,
故选:C.
点评 本题考查了利用导数研究函数的单调性、指数函数的单调性、复合命题真假的判定方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
12.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于P、Q两点,F2为右焦点,若△PQF2为等边三角形,则椭圆的离心率为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
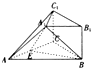 用如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.
用如图所示的几何体中,四边形BB1C1C是矩形,BB1⊥平面ABC,A1B1∥AB,AB=2A1B1,E是AC的中点.