题目内容
12.过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左焦点F1作x轴的垂线交椭圆于P、Q两点,F2为右焦点,若△PQF2为等边三角形,则椭圆的离心率为( )| A. | $\frac{\sqrt{2}}{2}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 设F1(-c,0),根据已知条件容易判断|PQ|与2c的关系,列出方程即可求出离心率.
解答 解:如图,设F1(-c,0),△PQF2为等边三角形,可得:$\frac{\sqrt{3}}{2}$•$\frac{2{b}^{2}}{a}$=2c,
∴2ca=$\sqrt{3}$b2=$\sqrt{3}$(a2-c2),可得2e=$\sqrt{3}$-$\sqrt{3}{e}^{2}$,
解得e=$\frac{\sqrt{3}}{3}$
∴该椭圆离心率为:$\frac{\sqrt{3}}{3}$.
故选:B.
点评 考查椭圆的标准方程,椭圆上的点和椭圆几何量的关系,椭圆的离心率及计算公式的应用.

练习册系列答案
相关题目
2.已知函数f(x)=alnx+$\frac{1}{x}$+2x在x=$\frac{1}{2}$处取得极值.
(1)求a的值;
(2)证明:f(x-1)>$\frac{e}{{e}^{x}}$+2x-2.
(1)求a的值;
(2)证明:f(x-1)>$\frac{e}{{e}^{x}}$+2x-2.
20.已知命题p:$?x∈({0,\frac{π}{2}}),sinx-x<0$,命题q:$?{x_0}∈({0,+∞}),{2^{x_0}}=\frac{1}{2}$,则下列命题为真命题的是( )
| A. | p∧q | B. | (¬p)∧(-q) | C. | p∧(¬q) | D. | (¬p)∧q |
17.过双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点F2(c,0)作圆x2+y2=a2的切线,切点为M,延长F2M交抛物线y2=-4cx于点P,其中O为坐标原点,若$\overrightarrow{OM}=\frac{1}{2}(\overrightarrow{O{F_2}}+\overrightarrow{OP})$,则双曲线的离心率为( )
| A. | $\frac{4\sqrt{2}-2}{7}$ | B. | $\frac{4\sqrt{2}+2}{7}$ | C. | $\frac{1+\sqrt{3}}{2}$ | D. | $\frac{1+\sqrt{5}}{2}$ |
4.F1、F2是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的两焦点,Q是椭圆上任一点,过一焦点引∠F1QF2的外角平分线的垂线,则垂足M的轨迹为( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
2.函数f(x)=ln(1-5x)的定义域是( )
| A. | (-∞,0) | B. | (0,1) | C. | (-∞,1) | D. | (0,+∞) |
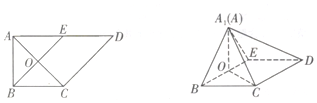 如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AD=2,AB=BC=1,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙
如图甲,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AD=2,AB=BC=1,E是AD的中点,O是AC与BE的交点,将△ABE沿BE折起到△A1BE的位置,如图乙