题目内容
18.在△ABC中,A,B,C的对边分别为a,b,c,a=10,$b=5\sqrt{7}$,且acosC,bcosB,ccosA成等差数列,则c=( )| A. | 15 | B. | 5 | C. | 3 | D. | 25 |
分析 先根据等差数列的性质,以及正弦定理和两角和的正弦公式求出B=60°,再根据余弦定理即可求出c的值.
解答 解、∵acosC、bcosB、ccosA成等差数列,
∴2bcosB=acosC+ccosA,
由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$=$\frac{c}{sinC}$,
∴2sinBcosB=sinAcosC+sinCcosA,
即2sinBcosB=sin(A+C)=sinB,
∵A,B,C为△ABC的内角,
∴sinB≠0,
∴cosB=$\frac{1}{2}$,
∴B=60°,
由余弦定理,可得b2=a2+c2-2accosB,a=10,$b=5\sqrt{7}$,
∴c2-10c-15=0,
解得c=15,
故选:A.
点评 本题考查了等差数列的性质,正弦定理和余弦定理,两角和的正弦公式,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知F1,F2分别是双曲线C:$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左,右焦点,M是C上的一点,且|MF2|=10,则|MF1|=( )
| A. | 10 | B. | 8 | C. | 4 | D. | 2 |
10.已知M、N分别是四面体OABC的棱OA,BC的中点,P点在线段MN上,且MP=2PN,设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则$\overrightarrow{OP}$=( )
| A. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | B. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | C. | $\frac{1}{6}$$\overrightarrow{a}$+$\frac{1}{3}$$\overrightarrow{b}$+$\frac{1}{3}$$\overrightarrow{c}$ | D. | $\frac{1}{3}$$\overrightarrow{a}$+$\frac{1}{6}$$\overrightarrow{b}$+$\frac{1}{6}$$\overrightarrow{c}$ |
7.已知点P(x,y)为圆x2+y2=1上的动点,则3x+4y的最小值为( )
| A. | 5 | B. | 1 | C. | 0 | D. | -5 |
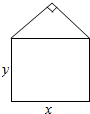 某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为4m2,问x,y分别为多少时用料最省?并求最省用料.
某单位用木料制作如图所示的框架,框架的下部是边长分别为x,y(单位:m)的矩形,上部是等腰直角三角形,要求框架围成的总面积为4m2,问x,y分别为多少时用料最省?并求最省用料.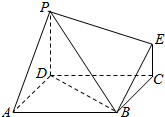 如图为一简单组合体,其底面ABCD为边长2正方形,PD⊥平面ABCD,EC∥PD,且$PD=2\sqrt{2},CE=\sqrt{2}$.
如图为一简单组合体,其底面ABCD为边长2正方形,PD⊥平面ABCD,EC∥PD,且$PD=2\sqrt{2},CE=\sqrt{2}$.  某校高中一年级组织学生参加了环保知识竞赛,并抽取了20名学生的成绩进行分析,如图是这20名学生竞赛成绩(单位:分)的频率分布直方图,其分组为[100,110),[110,120),…,[130,140),[140,150].
某校高中一年级组织学生参加了环保知识竞赛,并抽取了20名学生的成绩进行分析,如图是这20名学生竞赛成绩(单位:分)的频率分布直方图,其分组为[100,110),[110,120),…,[130,140),[140,150].