题目内容
16.函数f(x)=$\sqrt{{x}^{2}-7x+12}$的定义域是M,函数g(x)=$\frac{1}{lg(x-5)}$的定义域是N,则M和N的交集为{x|x>5,且x≠6}.分析 由x2-7x+12≥0,解得x,可得函数f(x)=$\sqrt{{x}^{2}-7x+12}$的定义域M.由x-5>0,且x-5≠1,解出可得函数g(x)=$\frac{1}{lg(x-5)}$的定义域.
解答 解:由x2-7x+12≥0,解得x≥4或x≤3,
∴函数f(x)=$\sqrt{{x}^{2}-7x+12}$的定义域M={x|x≥4或x≤3}.
由x-5>0,且x-5≠1,
解得x>5,且x-5≠1,
∴函数g(x)=$\frac{1}{lg(x-5)}$的定义域为N={x|x>5,且x≠6}.
∴M∩N={x|x>5,且x≠6}.
故答案为:{x|x>5,且x≠6}.
点评 本题考查了函数的定义域、不等式的性质、集合的运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
4.在△ABC中,角A,B,C所对应的边长分别为a、b、c,若asinA+bsinB=2csinC,则cosC的最小值为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
11.函数f(x)=$\left\{\begin{array}{l}{x-2(x≤1)}\\{{x}^{2}+1(x>1)}\end{array}\right.$,则f(3)=( )
| A. | 1 | B. | 4 | C. | 10 | D. | 2 |
1.下列函数中,为偶函数的是( )
| A. | y=4x2-2 | B. | y=5x-7 | C. | y=x2(x>0) | D. | y=(x-1)2 |
8.函数y=$\frac{2}{{x}^{2}-9}$的定义域是( )
| A. | (-3,3) | B. | {-3,3} | C. | {x|x≠±3} | D. | (-∞,-3)∪(3,+∞) |
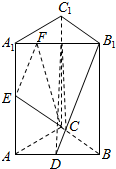 如图,在三棱柱ABC-A1B1C1中,D、E分别是AB、AA1的中点,AA1⊥平面ABC,AB⊥AC,AA1=4,AB=AC=2,且$\overrightarrow{{A}_{1}F}$=$\frac{1}{4}$$\overrightarrow{{A}_{1}{B}_{1}}$.
如图,在三棱柱ABC-A1B1C1中,D、E分别是AB、AA1的中点,AA1⊥平面ABC,AB⊥AC,AA1=4,AB=AC=2,且$\overrightarrow{{A}_{1}F}$=$\frac{1}{4}$$\overrightarrow{{A}_{1}{B}_{1}}$.