题目内容
已知复数z满足(1+
i)z=2
i（i为虚数单位），则z在复平面内对应的点位于（ ）
| 3 |
| 3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数的基本概念
专题：数系的扩充和复数
分析：由复数的除法运算化简复数z，得到对应点的坐标得答案．
解答：
解：由(1+
i)z=2
i，得
z=
=
=
=
+
i．
∴z在复平面内对应的点的坐标为(
，
)，是第一象限的点．
故选：A．
| 3 |
| 3 |
z=
2
| ||
1+
|
2
| ||||
(1+
|
6+2
| ||
| 4 |
| 3 |
| 2 |
| ||
| 2 |
∴z在复平面内对应的点的坐标为(
| 3 |
| 2 |
| ||
| 2 |
故选：A．
点评：本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
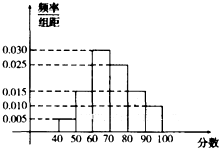某校从高一年级学生中随机抽取部分学生，将他们的模块测试成绩分成6组：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]加以统计，得到如图所示的频率分布直方图．已知高一年级共有学生500名，据此估计，该模块测试成绩不少于60分的学生人数为若α，β是非零实数，则“α+β=0”是“|α|+|β|＞0”成立的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
若α∈（
，π），则3cos2α=sin（
-α），则sin2α的值为（ ）
| π |
| 2 |
| π |
| 4 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知角α的终边经过点（12，-5），则sinα等于（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|