题目内容
已知函数f(x)=|x-1|+2|x-a|(a>1)
(1)当a=2时,解不等式f(x)≤5;
(2)若f(x)≥5恒成立,求实数a的取值范围.
(1)当a=2时,解不等式f(x)≤5;
(2)若f(x)≥5恒成立,求实数a的取值范围.
考点:函数恒成立问题
专题:综合题,函数的性质及应用
分析:(1)当a=2时,f(x)=|x-1|+2|x-2|,对x分类讨论,即可解不等式f(x)≤5;
(2)对x分类讨论,求出f(x)的最小值,利用f(x)≥5恒成立,可求实数a的取值范围.
(2)对x分类讨论,求出f(x)的最小值,利用f(x)≥5恒成立,可求实数a的取值范围.
解答:
解:(1)当a=2时,f(x)=|x-1|+2|x-2|.
当x<1时,-x+1-2x+4≤5,∴x≥0,∴0≤x<1;
当1≤x≤2时,x-1-2x+4≤5,∴x≥-2,∴1≤x≤2;
当x>2时,x-1+2x-4≤5,∴x≤
,∴2<x≤
,
∴不等式的解集为{x|0≤x≤
};
(2)当x<1时,f(x)=-x+1-2x+2a=-3x+2a+1>2a-2;
当1≤x≤a时,f(x)=x-1-2x+2a=-x+2a-1,∴a-1≤f(x)≤2a-2;
当x>a时,f(x)=x-1+2x-2a=3x-2a-1>a-1,
∵f(x)≥5恒成立,
∴a-1≥5,
∴a≥6.
当x<1时,-x+1-2x+4≤5,∴x≥0,∴0≤x<1;
当1≤x≤2时,x-1-2x+4≤5,∴x≥-2,∴1≤x≤2;
当x>2时,x-1+2x-4≤5,∴x≤
| 10 |
| 3 |
| 10 |
| 3 |
∴不等式的解集为{x|0≤x≤
| 10 |
| 3 |
(2)当x<1时,f(x)=-x+1-2x+2a=-3x+2a+1>2a-2;
当1≤x≤a时,f(x)=x-1-2x+2a=-x+2a-1,∴a-1≤f(x)≤2a-2;
当x>a时,f(x)=x-1+2x-2a=3x-2a-1>a-1,
∵f(x)≥5恒成立,
∴a-1≥5,
∴a≥6.
点评:本题考查绝对值不等式,考查恒成立问题,考查分类讨论是数学思想,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
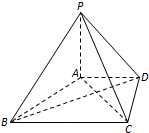 在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=
在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,BC=2AD=4,AB=CD=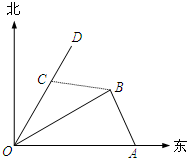 如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.
如图,港口A在港口O的正东120海里处,小岛B在港口O的北偏东60°的方向,且在港口A北偏西30°的方向上.一艘科学考察船从港口O出发,沿北偏东30°的OD方向以20海里/小时的速度驶离港口O.一艘给养快艇从港口A以60海里/小时的速度驶向小岛B,在B岛转运补给物资后以相同的航速送往科考船.已知两船同时出发,补给装船时间为1小时.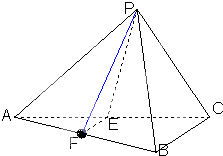 已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.
已知三棱锥P-ABC中,E.F分别是AC.AB的中点,△ABC,△PEF都是正三角形,PF⊥AB.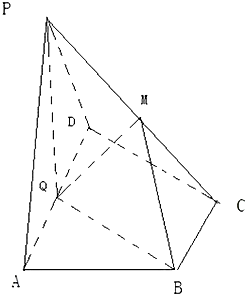 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,BC=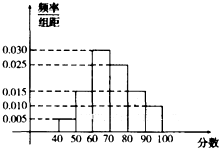 某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生500名,据此估计,该模块测试成绩不少于60分的学生人数为
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生500名,据此估计,该模块测试成绩不少于60分的学生人数为