题目内容
执行如图所示的程序图,若任意输入区间[1,19]中实数x,则输入x大于49的概率为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
考点:程序框图
专题:算法和程序框图
分析:根据框图的流程,依次计算运行的结果,直到不满足条件n≤3,求出输出x的值,再根据输出的x大于49,求出输入x的范围,根据几何概型的概率公式计算.
解答:
解:由程序框图知:第一次运行x=2x-1,n=2;
第二次运行x=2×(2x-1)-1.n=2+1=3;
第三次运行x=2×[2×(2x-1)-1]-1,n=3+1=4,
不满足条件n≤3,程序运行终止,输出x=8x-(4+2+1)=8x-7,
由输出的x大于49,得x>7,∴输入x∈(7,19],数集的长度为12,
又数集[1,19]的长度为18,
∴输出的x大于49的概率P=
=
.
故选:C
第二次运行x=2×(2x-1)-1.n=2+1=3;
第三次运行x=2×[2×(2x-1)-1]-1,n=3+1=4,
不满足条件n≤3,程序运行终止,输出x=8x-(4+2+1)=8x-7,
由输出的x大于49,得x>7,∴输入x∈(7,19],数集的长度为12,
又数集[1,19]的长度为18,
∴输出的x大于49的概率P=
| 12 |
| 18 |
| 2 |
| 3 |
故选:C
点评:本题考查了循环结构的程序框图,根据框图的流程判断算法的功能是解答此类问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设函数f(x)的定义域是R,若f(1-x)=f(1+x),且当x≥1时,f(x)=-
x3-2x+1,则有( )
| 1 |
| 3 |
A、f(
| ||||||
B、f(
| ||||||
C、f(
| ||||||
D、f(
|
已知集合A={x|x<-1或x≥3},则∁RA等于( )
| A、{x|x<3} |
| B、{x|x>-1} |
| C、{x|-1≤x<3} |
| D、∅ |
在等差数列{an}中,d=
,S100=145,则a1+a3+a5+…+a99的值为( )
| 1 |
| 2 |
| A、57 | B、58 | C、59 | D、60 |
设x,y,z表示直线(彼此不同)或平面(不重合),则“
⇒x∥y”成立的一个充分条件是( )
|
| A、x、y、z都是平面 |
| B、x、y、z都是直线 |
| C、x是直线,y、z是平面 |
| D、x、y是平面,z是直线 |
某几何体的三视图如图所示,则该几何体的表面积为( )
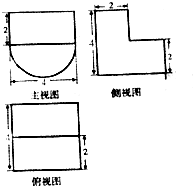

| A、40+12π |
| B、16+8π |
| C、16+16π |
| D、16+32π |