题目内容
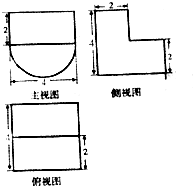
某几何体的三视图如图所示，则该几何体的表面积为（ ）
| A、40+12π |
| B、16+8π |
| C、16+16π |
| D、16+32π |
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体是半圆柱与长方体的组合体，根据三视图判断半圆柱与长方体的相关几何量的数据，把数据代入面积公式计算．
解答：
解：由三视图知：几何体是半圆柱与长方体的组合体，
且半圆柱的底面半径为2，母线长为4，
长方体的长、宽、高分别为4、2、2，
几何体的表面积S=S半圆柱侧面+S半圆柱底面+S长方体=π×2×4+π×22+4×2×4+2×2×2=8π+4π+32+8=40+12π．
故选：A．
且半圆柱的底面半径为2，母线长为4，
长方体的长、宽、高分别为4、2、2，
几何体的表面积S=S半圆柱侧面+S半圆柱底面+S长方体=π×2×4+π×22+4×2×4+2×2×2=8π+4π+32+8=40+12π．
故选：A．
点评：本题考查了由三视图求几何体的表面积，根据三视图判断几何体的形状及数据所对应的几何量是关键．
练习册系列答案
相关题目
若存在区间[m，n]，使得函数f（x）定义域为[m，n]时，其值域为[km，kn]（k∈N*），则称区间[m，n]为函数f（x）的“k倍区间”．已知函数f（x）=x3+sinx，则f（x）的“5倍区间”的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
（3x-
）n的展开式中各项系数之和为A，所有偶数项的二项式系数为B，若A+B=96，则展开式中的含有x2的项的系数为（ ）
| 1 | |||
|
| A、-540 | B、-180 |
| C、540 | D、180 |
已知复数z=
，其中i是虚数单位，则z的虚部为（ ）
| 2i |
| 1+i |
| A、2 | B、-2 | C、1 | D、-1 |
执行如图所示的程序图，若任意输入区间[1，19]中实数x，则输入x大于49的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
二项式（x2-
）n的展开式中各项系数的和为（ ）
| 1 |
| x |
| A、32 | B、-32 | C、0 | D、1 |
当0＜x＜
时，函数f（x）=
的最小值为（ ）
| π |
| 2 |
| 3sin2x+1 |
| tanxcos2x |
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|