题目内容
设函数f(x)的定义域是R,若f(1-x)=f(1+x),且当x≥1时,f(x)=-
x3-2x+1,则有( )
| 1 |
| 3 |
A、f(
| ||||||
B、f(
| ||||||
C、f(
| ||||||
D、f(
|
考点:函数单调性的性质,奇偶函数图象的对称性
专题:计算题,函数的性质及应用
分析:由f(1-x)=f(1+x),可得函数图象关于x=1对称,当x≥1时,函数单调递减,即可得出结论.
解答:
解:∵f(1-x)=f(1+x),
∴函数图象关于x=1对称,
∴f(
)=f(
),f(
)=f(
),
∵f(x)=-
x3-2x+1,
∴f′(x)=-x2-2,
∴当x≥1时,函数单调递减,
∵
>
>
,
∴f(
)>f(
)>f(
),
∴f(
)<f(
)<f(
).
故选:A.
∴函数图象关于x=1对称,
∴f(
| 1 |
| 3 |
| 5 |
| 3 |
| 3 |
| 4 |
| 5 |
| 4 |
∵f(x)=-
| 1 |
| 3 |
∴f′(x)=-x2-2,
∴当x≥1时,函数单调递减,
∵
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| 4 |
∴f(
| 5 |
| 4 |
| 4 |
| 3 |
| 1 |
| 3 |
∴f(
| 1 |
| 3 |
| 4 |
| 3 |
| 3 |
| 4 |
故选:A.
点评:本题主要考查了利用函数的单调性比较函数值大小,同时考查了运算求解的能力,属于基础题.

练习册系列答案
相关题目
在△ABC中,BC=3,AC=
,B=
,则△ABC的面积是( )
| 13 |
| π |
| 3 |
A、3
| ||||
B、6
| ||||
C、
| ||||
D、
|
集合M={(x,y)|x,y∈Z,ln2+ln(4-x)(4+y)≥2ln(y-x+6),则集合M的元素个数为( )
| A、13 | B、12 | C、11 | D、10 |
若存在区间[m,n],使得函数f(x)定义域为[m,n]时,其值域为[km,kn](k∈N*),则称区间[m,n]为函数f(x)的“k倍区间”.已知函数f(x)=x3+sinx,则f(x)的“5倍区间”的个数是( )
| A、0 | B、1 | C、2 | D、3 |
已知log2(x+2)=2,则x等于( )
| A、-1 | B、0 | C、2 | D、6 |
已知i是虚数单位,且z=(
)2014+i的共轭复数为
,则z•
等于( )
| 1-i |
| 1+i |
. |
| z |
. |
| z |
| A、2 | B、1 | C、0 | D、-1 |
执行如图所示的程序图,若任意输入区间[1,19]中实数x,则输入x大于49的概率为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
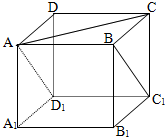 如图,正方体ABCD-A1B1C1D1中,点P是直线BC1的动点,则下列四个命题:
如图,正方体ABCD-A1B1C1D1中,点P是直线BC1的动点,则下列四个命题: