题目内容

证明函数g(x)=
ex+e-x
2
的奇偶性，并求定义域和值域．
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：利用函数的奇偶性定义，证明即可，定义域为全体实数，利用基本不等式求出g（x）的最小值，值域即可求．
解答： 解：∵g（-x）=
e-x+ex
2
=g（x），
∴g（x）为偶函数，
定义域为（-∞，+∞）
∵
e-x+ex
2
≥
1
2
×2
ex•e-x 
=1，当且仅当x=0时取等号，
∴值域为（1，+∞）
点评：本题考查了函数的奇偶性，定义域，值域，关键利用基本不等式求值域方便．
练习册系列答案
相关题目
已知：各项均为正数的数列{an}的前n项和为Sn，且对任意正整数n，点（an，Sn）都在直线2x-y-
1
2
=0上．
（1）求数列{an}的通项公式．
（2）（附加题）若an2=2-b，设Cn=
bn
an
  求：数列{Cn}前n项和Tn．
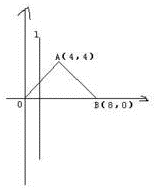如图，直线l⊥x轴，从原点开始向右平行移动到x=8处停止，它扫过△AOB所得图形的面积为S，它与x轴的交点为（x，0）．
（1）求函数S=f（x）的解析式；
（2）求函数S=f（x）的定义域、值域；
（3）作函数S=f（x）的图象．
已知函数y=f（x）=2
3
sinxcos+2cos2x+a（x∈R），其中a为常数．
（1）求函数y=f（x）的周期；
（2）如果y=f（x）的最小值为0，求a的值，并求此时f（x）的最大值及图象的对称轴方程．
已知△ABC的两边b、c是方程x2-kx+40=0的两根，△ABC的面积是10
3
，周长是20，试求∠A和k的值．
已知命题p：x（x-5）＜0；命题q：函数y=log2（x2-x-12）有意义．
（1）若p∧q为真命题，求实数x的取值范围；
（2）若￢p∧q为真命题，求实数x的取值范围．
给定下列命题：
①“x＞1”是“x＞2”的充分不必要条件；
②“若sinα≠
1
2
，则α≠
π
6
”；
③若xy=0，则x=0且y=0”的逆否命题；
④命题“?x0∈R，使x02-x0+1≤0”的否定．
其中真命题的序号是
 
．
在等比数列{an}中，a2+a3=1，a3+a4=-2，则a5+b6=
 
．
若函数f（x）=x2-8lnx在其定义域内的一个子区间（k-1，k+1）内是单调函数，则实数k的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网