题目内容
若函数f(x)=x2-8lnx在其定义域内的一个子区间(k-1,k+1)内是单调函数,则实数k的取值范围是 .
考点:函数的单调性与导数的关系
专题:导数的综合应用
分析:先确定函数的定义域然后求导数fˊ(x),在函数的定义域内解方程fˊ(x)=0,求出f(x)的单调区间,根据子区间(k-1,k+1)是单调函数,建立不等关系,解之即可.
解答:
解:∵f(x)定义域为(0,+∞),
∴f′(x)=2x-
=
,
令f′(x)=0,解得,x=2,
当f′(x)<0时,f(x)在(0,2)单调递减,
当f′(x)>0时,f(x)在(2,+∞)单调递增,
∵f(x)在(k-1,k+1)内是单调函数,
∴
,或k-1≥2,
解得,k=1或k≥3.
故答案为:{1}∪[3,+∞),
∴f′(x)=2x-
| 8 |
| x |
| 2(x+2)(x-2) |
| x |
令f′(x)=0,解得,x=2,
当f′(x)<0时,f(x)在(0,2)单调递减,
当f′(x)>0时,f(x)在(2,+∞)单调递增,
∵f(x)在(k-1,k+1)内是单调函数,
∴
|
解得,k=1或k≥3.
故答案为:{1}∪[3,+∞),
点评:题主要考查了对数函数的导数,以及利用导数研究函数的单调性等基础知识,考查计算能力,对于利用导数研究函数的单调性,注意导数的正负对应着函数的单调性.属于基础题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
一个长方体被一平面截去一部分所得几何体的三视图如图,则该几何体的体积是( )


| A、1440 | B、1200 |
| C、960 | D、720 |
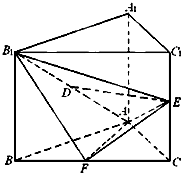 已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点. 矩形ABCD中,AB=6,BC=2
矩形ABCD中,AB=6,BC=2