题目内容
13.设数列{an}(n=1,2,3…)的前n项和Sn满足Sn=2an-a1,且a1,a2+1,a3成等差数列.(1)求数列的通项公式;
(2)设bn=$\frac{({a}_{n})^{2}-1}{{S}_{n}}$,数列{bn}的前n项和为Tn,求Tn.
分析 (1)由条件Sn满足Sn=2an-a1,求得数列{an}为等比数列,且公比q=2;再根据a1,a2+1,a3成等差数列,求得首项的值,可得数列{an}的通项公式;
(2)由Sn=2an-a1,求得数列{bn}的通项公式,根据等比数列前n项和公式,即可求得数列{bn}的前n项和为Tn.
解答 解:(1)由已知Sn=2an-a1,
当n≥2,Sn-1=2an-1-a1,
两式相减得an=2an-2an-1,即an=2an-1(n≥2),
从而a2=2a1,a3=2a2=4a1,
∵a1,a2+1,a3成等差数列,即a1+a3=2(a2+1),
∴a1+4a1=2(2a1+1),解得a1=2,
∴数列{an}是首项为2,公比为2的等比数列,
数列{an}的通项公式an=2n;
(2)由(1)可知a1=2,Sn=2an-a1=2n+1-2,
bn=$\frac{({a}_{n})^{2}-1}{{S}_{n}}$=$\frac{({2}^{n}-1)({2}^{n}+1)}{2({2}^{n}-1)}$=2n-1+$\frac{1}{2}$,
数列{bn}的前n项和为Tn,Tn=$\frac{1-{2}^{n}}{1-2}$+$\frac{1}{2}$n,
=2n+$\frac{1}{2}$n-1,
∴数列{bn}的前n项和为Tn,Tn=2n+$\frac{1}{2}$n-1.
点评 本题考查了错位相减法、等比数列的通项公式与求和公式、数列递推关系,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
相关题目
4.已知实数x,y满足$\left\{\begin{array}{l}x+y≤1\\ x-y≤1\\ x≥0\end{array}\right.$,且目标函数z=ax+2y的最大值为2,则实数a的取值范围为( )
| A. | (-∞,0] | B. | (-∞,2] | C. | 10,+∞) | D. | 12,+∞) |
18.计算$\int_0^2{({\sqrt{4-{x^2}}-2x})dx=}$( )
| A. | 2π-4 | B. | π-4 | C. | ln2-4 | D. | ln2-2 |
5.等比数列{an}中,a2,a6是方程x2-34x+81=0的两根,则a4等于( )
| A. | 9 | B. | -9 | C. | ±9 | D. | 以上都不对 |
2.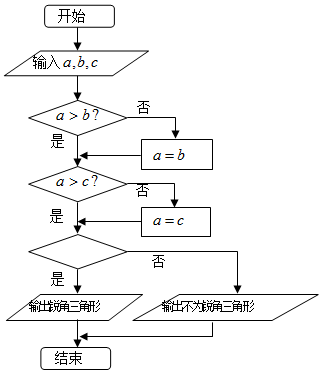 下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( )
下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( )
 下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( )
下面程序框图中,若输入互不相等的三个正实数a,b,c(abc≠0),要求判断△ABC的形状,则空白的判断框应填入( )| A. | a2+b2>c2? | B. | a2+c2>b2? | C. | b2+c2>a2? | D. | b2+a2=c2? |
3.函数f(x)是定义在(-∞,+∞)内的可导函数,且满足:xf'(x)+f(x)>0,对于任意的正实数a,b,若a>b,则必有( )
| A. | af(b)>bf(a) | B. | bf(a)>af(b) | C. | af(a)<bf(b) | D. | af(a)>bf(b) |