题目内容
已知f(x)=2cos2x+2
sinxcosx-1
(1)求函数y=f(x)的最小正周期及其图象的对称中心;
(2)求函数f(x)在区间[0,
]上的取值范围;
(3)若x∈[0,m]时,有y=f(x)的值域为[1,2],求实数m的取值范围.
| 3 |
(1)求函数y=f(x)的最小正周期及其图象的对称中心;
(2)求函数f(x)在区间[0,
| 2π |
| 3 |
(3)若x∈[0,m]时,有y=f(x)的值域为[1,2],求实数m的取值范围.
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的图像与性质
分析:(1)利用三角函数的倍角公式以及辅助角公式将函数进行化简求函数y=f(x)的最小正周期及其图象的对称中心;
(2)根据三角函数的图象和性质,求函数f(x)在区间[0,
]上的取值范围;
(3)若x∈[0,m]时,求出2x+
的范围,结合y=f(x)的值域为[1,2],即可求实数m的取值范围.
(2)根据三角函数的图象和性质,求函数f(x)在区间[0,
| 2π |
| 3 |
(3)若x∈[0,m]时,求出2x+
| π |
| 6 |
解答:
解:(1)f(x)=2cos2x+2
sinxcosx-1=cos2x+
sin2x=2sin(2x+
)
则函数y=f(x)的最小正周期T=
=π,
由2x+
=kπ,解得x=
-
,k∈Z,
即函数图象的对称中心为(
-
,0)k∈Z;
(2)∵0≤x≤
,∴0≤2x≤
,
≤2x+
≤
,则1≤2sin(2x+
)≤2,
即函数f(x)在区间[0,
]上的取值范围是[1,2];
(3)若x∈[0,m]时,则0≤2x≤2m,
≤2x+
≤2m+
,
∵当2x+
=
时,f(x)=2sin(2x+
)=1,
若y=f(x)的值域为[1,2],
则
≤2m+
≤
,
即
≤m≤
,
即实数m的取值范围是[
,
].
| 3 |
| 3 |
| π |
| 6 |
则函数y=f(x)的最小正周期T=
| 2π |
| 2 |
由2x+
| π |
| 6 |
| kπ |
| 2 |
| π |
| 12 |
即函数图象的对称中心为(
| kπ |
| 2 |
| π |
| 12 |
(2)∵0≤x≤
| 2π |
| 3 |
| 4π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
| π |
| 6 |
即函数f(x)在区间[0,
| 2π |
| 3 |
(3)若x∈[0,m]时,则0≤2x≤2m,
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
∵当2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
若y=f(x)的值域为[1,2],
则
| π |
| 2 |
| π |
| 6 |
| 5π |
| 6 |
即
| π |
| 6 |
| π |
| 3 |
即实数m的取值范围是[
| π |
| 6 |
| π |
| 3 |
点评:本题主要考查三角函数的图象和性质,利用辅助角公式将函数进行化简,考查学生的运算能力.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
等差数列{an}的前n项和为Sn.且S3=6,a3=0,则公差d等于( )
| A、2 | B、1 | C、-1 | D、-2 |
下面的流程图表示的算法执行的结果是( )


| A、5050 | B、2550 |
| C、2450 | D、2500 |
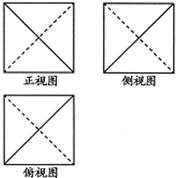 某几何体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此几何体的外接球的表面积为( )
某几何体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此几何体的外接球的表面积为( )| A、3π | ||
| B、4π | ||
| C、2π | ||
D、
|
向量
=(-1,1),且
与
+2
方向相同,则
•
的范围是( )
| a |
| a |
| a |
| b |
| a |
| b |
| A、(1,+∞) |
| B、(-1,1) |
| C、(-1,+∞) |
| D、(-∞,1) |
已知等差数列{an},a1=1,a3=3,则数列{
}的前10项和为( )
| 1 |
| anan+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|