题目内容
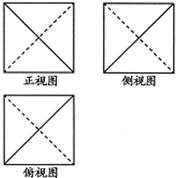 某几何体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此几何体的外接球的表面积为( )
某几何体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此几何体的外接球的表面积为( )| A、3π | ||
| B、4π | ||
| C、2π | ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:如图所示,该几何体是正方体的内接正四棱锥.因此此几何体的外接球的直径2R=正方体的对角线
,利用球的表面积计算公式即可得出.
| 3 |
解答:
解:如图所示,该几何体是正方体的内接正四棱锥.
因此此几何体的外接球的直径2R=正方体的对角线
,
其表面积S=4πR2=3π.
故选:A.

因此此几何体的外接球的直径2R=正方体的对角线
| 3 |
其表面积S=4πR2=3π.
故选:A.
点评:本题考查了正方体的内接正四棱锥、球的表面积计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
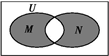 已知全集U=R,集合M={x|y=
已知全集U=R,集合M={x|y=| 3-x2 |
| π |
| 4 |
A、[-3,-
| ||||
B、(1,
| ||||
C、[-3,-
| ||||
D、[-3,-
|
|2x+2|-|2x-2|≤a恒成立,则实数a的取值范围是( )
| A、(-∞,-4) |
| B、[4,+∞) |
| C、[-4,+∞) |
| D、(-4,+∞) |
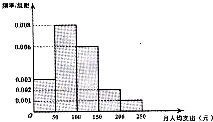 如图为某市地铁乘客的月人均乘坐地铁费用支出的频率分布直方图,若按直方图中的五段分层,并使用分层抽样方法从该市地铁乘客中抽取40人参加听证会,则所抽取的40人中月人均乘坐地铁费用支出在[100,150)的人数为( )
如图为某市地铁乘客的月人均乘坐地铁费用支出的频率分布直方图,若按直方图中的五段分层,并使用分层抽样方法从该市地铁乘客中抽取40人参加听证会,则所抽取的40人中月人均乘坐地铁费用支出在[100,150)的人数为( )| A、4 | B、8 | C、12 | D、16 |
如果对定义在R上的函数f(x),对任意两个不相等的实数x1,x2,都有x1(f(x1)-f(x2))>x2(f(x1)-f(x2)),则称函数f(x)为“H函数”.下列函数是“H函数”的是( )
| A、y=x2 |
| B、y=-ex+1 |
| C、y=2x-sinx |
| D、y=lg|x| |
设方程x2+y2+2ax+2by+a2=0表示圆,则下列点中,必位于圆外的点是( )
| A、(0,0) |
| B、(1,0) |
| C、(a,b) |
| D、(a,-b) |
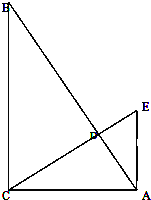 △ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.
△ABC中,∠BCA=90°,AB=1,过C作CD⊥AB于D,过A作AE⊥AC,CD的延长线交AE于E,设∠B=θ,θ是变量.