题目内容
曲线y=x+
（x＜0）的单调递增区间为（ ）
| 1 |
| x |
| A、（-∞，-1） |
| B、（-1，0） |
| C、（-∞，0） |
| D、（-∞，-4） |
考点：利用导数研究函数的单调性
专题：导数的概念及应用
分析：先求出函数的导数，解不等式求出即可．
解答：
解：∵y′=1-
，（x＜0），
令y′＞0，解得：x＜-1或，x＞1（舍），
∴曲线y=x+
（x＜0）的单调递增区间为（-∞，-1），
故选：A．
| 1 |
| x2 |
令y′＞0，解得：x＜-1或，x＞1（舍），
∴曲线y=x+
| 1 |
| x |
故选：A．
点评：本题考查了函数的单调性，导数的应用，是一道基础题．
练习册系列答案
相关题目
若数列{an}的通项公式an=（-1）n（2n+1），其前n项和为Sn，则S10=（ ）
| A、10 | B、-10 |
| C、12 | D、-12 |
设等差数列{an}的前n项和Sn，若S15＞0，S16＜0，则数列{
}的前15项中最大的项是（ ）
| Sn |
| an |
| A、第1项 | B、第8项 |
| C、第9项 | D、第15项 |
三菱柱的侧棱与底面垂直，且底面是边长为2的等边三角形，其正视图（如图）的面积为8，则该三棱柱的体积为（ ）| A、4 | ||
B、4
| ||
C、8
| ||
| D、16 |
若抛物线x2=2py的焦点与椭圆
+
=1的下焦点重合，则p的值为（ ）
| x2 |
| 3 |
| y2 |
| 4 |
| A、4 | B、2 | C、-4 | D、-2 |
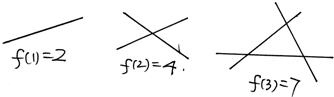对于问题：“两两相交且任三条不共点的n条直线把平面分为f（n）部分”，我们由归纳推理得到f（10）=（ ）| A、54 | B、55 | C、56 | D、57 |
下列说法正确的是（ ）
| A、函数的极大值就是函数的最大值 |
| B、函数的极小值就是函数的最小值 |
| C、函数的最值一定是极值 |
| D、在闭区间上的连续函数一定存在最值 |
在△ABC中，若a=7，b=8，cosC=
，则c=（ ）
| 13 |
| 14 |
| A、1 | B、2 | C、3 | D、4 |