题目内容
若抛物线x2=2py的焦点与椭圆
+
=1的下焦点重合，则p的值为（ ）
| x2 |
| 3 |
| y2 |
| 4 |
| A、4 | B、2 | C、-4 | D、-2 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用椭圆和抛物线的简单性质直接求解．
解答：
解：椭圆
+
=1的下焦点坐标分别为（0，-1），
∵抛物线x2=2py的焦点与椭圆
+
=1的下焦点重合，
∴
=-1，
∴p=-2．
故选：D．
| x2 |
| 3 |
| y2 |
| 4 |
∵抛物线x2=2py的焦点与椭圆
| x2 |
| 3 |
| y2 |
| 4 |
∴
| p |
| 2 |
∴p=-2．
故选：D．
点评：本题考查抛物线中参数的求法，是基础题，解题时要注意椭圆线和抛物线的简单性质的合理运用．
练习册系列答案
阅读快车系列答案
相关题目
在△ABC中，内角A，B，C的对边分别为a，b，c，若a=18，b=24，A=45°，则这样的三角形有（ ）
| A、0个 | B、两个 |
| C、一个 | D、至多一个 |
已知数列a1=2中，a1=2，an+1=an+
（n∈N*），则a101的值（ ）
| 1 |
| 2 |
| A、50 | B、51 | C、52 | D、53 |
下列双曲线不是以2x±3y=0为渐近线的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
先后抛掷红、蓝两枚骰子，事件A：红骰子出现3点，事件B：蓝骰子出现的点数为奇数，则P（A|B）=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
曲线y=x+
（x＜0）的单调递增区间为（ ）
| 1 |
| x |
| A、（-∞，-1） |
| B、（-1，0） |
| C、（-∞，0） |
| D、（-∞，-4） |
已知α为锐角，且sin（α-
）=
，则sinα=（ ）
| π |
| 4 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
利用基本不等式求最值，下列各式运用正确的是（ ）
A、y=x+
| ||||||
B、y=sinx+
| ||||||
C、y=3x+
| ||||||
D、y=lgx+4logx10≥2
|
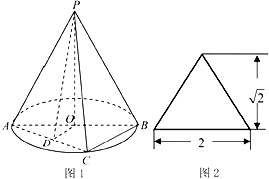圆锥PO如图1所示，图2是它的正（主）视图．已知圆O的直径为AB，C是圆周上异于A、B的一点，D为AC的中点