题目内容
设等差数列{an}的前n项和Sn，若S15＞0，S16＜0，则数列{
}的前15项中最大的项是（ ）
| Sn |
| an |
| A、第1项 | B、第8项 |
| C、第9项 | D、第15项 |
考点：数列的求和
专题：等差数列与等比数列
分析：等差数列前n项和Sn=（
）n2+（a1-
）n，由已知条件得a8＞0，a9＜0，d＜0，Sn最大值是S8，由此推导出
最大．
| d |
| 2 |
| d |
| 2 |
| S8 |
| a8 |
解答：
解：∵等差数列前n项和Sn=（
）n2+（a1-
）n，
由S15＞0，S16＜0，得a1+7d＞0，a1+
d＜0，
∴a8＞0，a9＜0，d＜0，
若视为函数则对称轴在S8和S9之间，
∵S8＞S9，∴Sn最大值是S8，
分析
，知an为正值时有最大值，故为前8项，
又d＜0，an递减，前8项中Sn递增，
∴前8项中Sn最大an最小时
有最大值，
∴
最大．
故选：B．
| d |
| 2 |
| d |
| 2 |
由S15＞0，S16＜0，得a1+7d＞0，a1+
| 15 |
| 2 |
∴a8＞0，a9＜0，d＜0，
若视为函数则对称轴在S8和S9之间，
∵S8＞S9，∴Sn最大值是S8，
分析
| Sn |
| an |
又d＜0，an递减，前8项中Sn递增，
∴前8项中Sn最大an最小时
| Sn |
| an |
∴
| S8 |
| a8 |
故选：B．
点评：本题考查数列{
}的前15项中最大的项的求法，是中档题，解题时要注意审题，注意等差数列的性质的合理运用．
| Sn |
| an |
练习册系列答案
相关题目
设A，B，C为圆O上三点，且AB=3，AC=5，则
•
=（ ）
| AO |
| BC |
| A、-8 | B、-1 | C、1 | D、8 |
设a是在区间[-3，0]上的任意一个实数，b是在区间[-2，0]上任意一个实数，则使原点到直线（a+1）x-（1-b）y+
=0的距离不大于1的概率为（ ）
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上都不对 |
已知数列a1=2中，a1=2，an+1=an+
（n∈N*），则a101的值（ ）
| 1 |
| 2 |
| A、50 | B、51 | C、52 | D、53 |
将一个骰子抛掷一次，设事件A表示向上的一面出现的点数不超过3，事件B表示向上的一面出现的点数不小于4，事件C表示向上的一面出现奇数点，则（ ）
| A、A与B是互斥而非对立事件 |
| B、A与B是对立事件 |
| C、B与C是互斥而非对立事件 |
| D、B与C是对立事件 |
下列双曲线不是以2x±3y=0为渐近线的是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
曲线y=x+
（x＜0）的单调递增区间为（ ）
| 1 |
| x |
| A、（-∞，-1） |
| B、（-1，0） |
| C、（-∞，0） |
| D、（-∞，-4） |
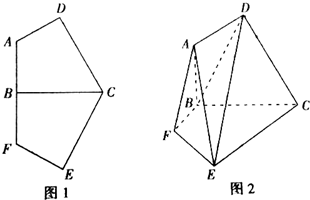已知平面内有一个五边形ABCEF，且关于线段BC对称（如图1所示），FE⊥CE，BF=FE=1，CB=CE=