题目内容
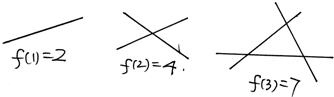 对于问题:“两两相交且任三条不共点的n条直线把平面分为f(n)部分”,我们由归纳推理得到f(10)=( )
对于问题:“两两相交且任三条不共点的n条直线把平面分为f(n)部分”,我们由归纳推理得到f(10)=( )| A、54 | B、55 | C、56 | D、57 |
考点:归纳推理
专题:推理和证明
分析:一条直线把平面分成2部分,两条直线把平面分成2+2=4部分,三条直线把平面分成2+2+3=7部分,四条直线把平面分成2+2+3+4=11部分,即n条直线把平面分成2+2+3+4+5+…=1+1+2+3+…+n=1+
部分,问题得以解决.
| n(n+1) |
| 2 |
解答:
解:一条直线把平面分成2部分,即f(1)=2=1+1,
两条直线把平面分成2+2=4部分,即f(2)=4=1+1+2,
三条直线把平面分成2+2+3=7部分,即f(3)=7=1+1+2+3,
四条直线把平面分成2+2+3+4=11部分,即f(4)=11=1+1+2+3+4,
于是可以得出:
即n条直线把平面分成f(n)=2+2+3+4+5+…=1+1+2+3+…+n=1+
部分,
故f(10)=1+
=56.
故选:C.
两条直线把平面分成2+2=4部分,即f(2)=4=1+1+2,
三条直线把平面分成2+2+3=7部分,即f(3)=7=1+1+2+3,
四条直线把平面分成2+2+3+4=11部分,即f(4)=11=1+1+2+3+4,
于是可以得出:
即n条直线把平面分成f(n)=2+2+3+4+5+…=1+1+2+3+…+n=1+
| n(n+1) |
| 2 |
故f(10)=1+
| 10(10+1) |
| 2 |
故选:C.
点评:本题考查了直线、射线、线段的应用,关键是能根据已知得出的结论总结出规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线
-
=1(a>0,b>0)以及双曲线
-
=1(a>0,b>0)的渐近线将第一象限三等分,则双曲线
-
=1的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| a2 |
| x2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
A、2或
| ||||||
B、
| ||||||
C、
| ||||||
D、2或
|
将一个骰子抛掷一次,设事件A表示向上的一面出现的点数不超过3,事件B表示向上的一面出现的点数不小于4,事件C表示向上的一面出现奇数点,则( )
| A、A与B是互斥而非对立事件 |
| B、A与B是对立事件 |
| C、B与C是互斥而非对立事件 |
| D、B与C是对立事件 |
曲线y=x+
(x<0)的单调递增区间为( )
| 1 |
| x |
| A、(-∞,-1) |
| B、(-1,0) |
| C、(-∞,0) |
| D、(-∞,-4) |
已知函数f(x)=
x2-ax+lnx在(0,+∞)上是增函数,则a的取值范围是( )
| 1 |
| 2 |
| A、(-∞,2) |
| B、(-∞,2] |
| C、(-2,2) |
| D、[-2,2] |
323和391的最大公约数是( )
| A、21 | B、19 | C、17 | D、13 |