题目内容
已知等差数列的前n项和为18,若S3=1,an+an-1+an-2=3,则n的值为( )
| A、9 | B、21 | C、27 | D、36 |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由等差数列的前n项和为18,S3=1,an+an-1+an-2=3,推导出a1+an=
,由此能求出n的值.
| 4 |
| 3 |
解答:
解:∵等差数列的前n项和为18,S3=1,an+an-1+an-2=3,
∴a1+a2+a3+an+an-1+an-2=3(a1+an)=4,
∴a1+an=
,
∴Sn=
(a1+an)=18,
∴
=18×
=18×
,
解得n=27.
故选:C.
∴a1+a2+a3+an+an-1+an-2=3(a1+an)=4,
∴a1+an=
| 4 |
| 3 |
∴Sn=
| n |
| 2 |
∴
| n |
| 2 |
| 1 |
| a1+an |
| 3 |
| 4 |
解得n=27.
故选:C.
点评:本题考查等差数列的前n项和公式的应用,解题时要认真审题,推导出a1+an=
是解题的关键.
| 4 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过抛物线y2=4x的焦点作一条直线与抛物线相交于A、B两点,它们的横坐标之和等于2,则这样的直线( )
| A、有且仅有一条 |
| B、有且仅有两条 |
| C、有无穷多条 |
| D、不存在 |
设集合A={y|y=x2-2x},B={x|y=log2(3-x),则A∩B=( )
| A、∅ | B、(-1,3) |
| C、[-1,3) | D、[-1,3] |
已知圆(x-1)2+(y-3
)2=r2(r>0)的一条切线y=kx+
与直线x=5的夹角为
,则半径r的值为( )
| 3 |
| 3 |
| π |
| 6 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知集合A={x||x|>1},B={x|x2+x-6≤0},则集合A∩B=( )
| A、{x|-3≤x<-1或1<x≤2} |
| B、{x|-3≤x<-1或x>1} |
| C、{x|-3≤x<-1或1≤x<2} |
| D、{x|x<-3或1<x≤2} |
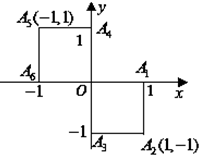 小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球;若X=0就去唱歌;若X<0就去下棋.
小波以游戏方式决定:是去打球、唱歌还是去下棋.游戏规则为:以O为起点,再从A1,A2,A3,A4,A5,A6(如图)这6个点中任取两点分别为终点得到两个向量,记这两个向量的数量积为X,若X>0就去打球;若X=0就去唱歌;若X<0就去下棋.