题目内容
已知函数f(x)=
,若f(2-a)>f(a),则实数a的取值范围是( )
|
| A、(-∞,2) |
| B、(-∞,1) |
| C、(1,2) |
| D、(-∞,-1) |
考点:分段函数的应用
专题:计算题,函数的性质及应用
分析:由题意,按a>2,0≤a≤2,a<0三种情况讨论即可.
解答:
解:①若a>2,则2-a<0,
故f(2-a)>f(a)可化为
4(2-a)-(2-a)2>4a+a2,
即a2+2a-2<0,
∵a>2,∴a2+2a-2<0无解;
②当0≤a≤2时,
f(2-a)>f(a)可化为4(2-a)+(2-a)2>4a+a2,
即a<1,
故0≤a<1;
③当a<0时,f(2-a)>f(a)可化为4(2-a)+(2-a)2>4a-a2,
即a2-6a+6>0,其在a<0时显然成立,
综上所述,a<1;
故选B.
故f(2-a)>f(a)可化为
4(2-a)-(2-a)2>4a+a2,
即a2+2a-2<0,
∵a>2,∴a2+2a-2<0无解;
②当0≤a≤2时,
f(2-a)>f(a)可化为4(2-a)+(2-a)2>4a+a2,
即a<1,
故0≤a<1;
③当a<0时,f(2-a)>f(a)可化为4(2-a)+(2-a)2>4a-a2,
即a2-6a+6>0,其在a<0时显然成立,
综上所述,a<1;
故选B.
点评:本题考查了分段函数的应用,属于中档题.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
已知数列{xn}满足xn+3=xn,xn+2=|xn+1-xn|(n∈N*),若x1=1,x2=a(a≤1且a≠0),则数列{xn}的前2016项的和等于( )
| A、671 | B、760 |
| C、1324 | D、1344 |
下列命题错误的是( )
| A、在△ABC中,“A>B”是“sinA>sinB”的充要条件 | ||||||||||||
B、点(
| ||||||||||||
C、若|
| ||||||||||||
| D、“sinα=sinβ”的充要条件是“α+β=(2k+1)π或α-β=2kπ(k∈Z)” |
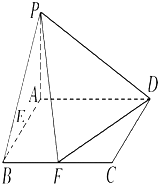 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.